A phenomenon you usually hear can now be seen in stars' rotation, and it may help untangle the mysteries of their magnetic fields.

The Sun observed in visible (left) and ultraviolet light (right). Sunspots, seen as dark patches in visible wavelengths, are sites of tightly coiled magnetic loops. These heat the Sun's upper atmosphere and show up as bright areas in the UV.
Mark Zastrow
“Listen to the beats,” my childhood violin teacher told me as she taught me to tune my instrument. You mean, like the rhythm? I thought.
She played two of her strings, releasing, broad resonant tones. But underneath, I could heard something like this:
wuhh…wuhh…wuhh…
That “beating” effect is caused by the sound of two slightly different frequencies interfering with each other and helps musicians stay in tune. But a recent study from a pair of researchers at the University of Göttingen in Germany is an example of how the beating effect might help astronomers, too.
Appearing in an upcoming Astronomy & Astrophysics, the work uses computer simulations to show how photometric data of a star’s brightness — like those collected by the planet-hunting satellites COROT (recently retired) and Kepler (which likely will be, too) — contain the beating signature of starspots. When analyzed, it can reveal multiple spots in different locations on a star, and may help to unravel the mysteries around their magnetic fields.
Meet the Soundtrack
It’s easiest to demonstrate this beating by showing them as acoustic waveforms. Here is one second of two close frequencies:
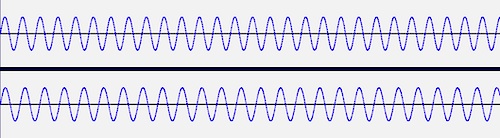
Mark Zastrow
They may look similar, but the top one has a frequency of 30 Hz and the bottom is 27 Hz. So although they start neatly aligned, as they slip out of alignment, the waves begin to cancel each other out instead of augmenting each other. You can see what I mean when we combine the two tracks: they look like this…

Intern A (Mark Zastrow)
…and sound like dubstep:
What does this have to do with starspots?
Starspots are indicators of magnetic activity: they are caused by twisted coils of magnetic field so tightly knotted that they suppress a star’s own radiant energy. We see them often on the Sun, but they are difficult to measure directly on distant stars. A big patch of them on a star’s surface can temporarily dim the visible light by as much as a few percent, at least until the spots rotate out of view (or to a star’s dimmer edge). Plotting the brightness over time in a light curve can produce a wavelike graph:
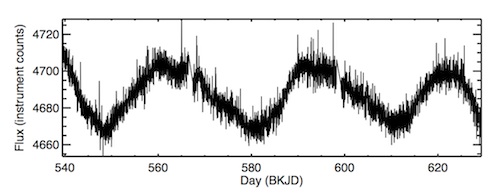
Light curve of Kepler Object of Interest 2156
Intern A (Mark Zastrow)
The frequency of this light-curve “wave” is how fast the star rotates. One important piece of information this reveals is a sense of its age. Over time, a star loses some of its angular momentum to the particles of the stellar wind that it blows into space. Like a figure skater throwing out her arms, the star slowly spins down.
Beats by DR (differential rotation)
But a star like the Sun doesn’t have one rotational frequency. Its gas behaves as a fluid, circulating from interior to surface and back again in a layer reaching down one-third of the way to its core. Because of the angular momentum that is transferred, the hot, charged gas races around the Sun’s equator in 25 days, but it takes a leisurely 34 days to circle the poles. The “differential rotation” of this plasma was first discovered by Richard Carrington using his own sunspot observations in 1863. Scientists suspect it is a key part of the motor that keeps Sun-like stars’ magnetic fields going, especially deep in the interior at the boundary of the convective layer (called the tachocline), which shears against the rigidly rotating layer below.
Fast forward to 2009, when the COROT and Kepler satellites began sending back light curves like this:
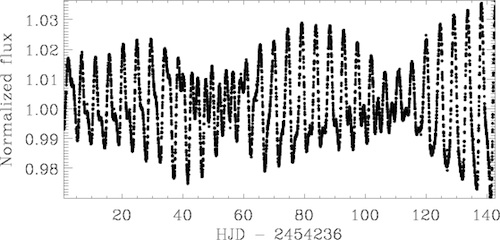
Mark Zastrow
This plot of the star COROT–2 instantly betrays differential rotation: starspots at different latitudes produce “waves” of differing periods that beat against one another. Identifying the frequencies gives a lower limit on the range of rotation speeds present on the star’s surface.
The new study out of Göttingen presents a simple method to identify these frequencies. The researchers tested their method using simulated light curves from model stars covered in spots (many less obvious than COROT–2’s). They find that roughly two-thirds of the time, they could tease apart the effect of multiple spots, giving an indication of differential rotation.
While not yet perfect, the method could take advantage of the vast amount of data in Kepler’s archives, which is a treasure-trove not only for planet hunters but stellar physicists, too.
“With Kepler it becomes now possible to study the surface flows on thousands of other stars in great detail, something we could only dream of a few years ago,” says study coauthor Timo Reinhold.
M dwarfs are of particular interest. The smallest of them are fully convective, meaning their layer of up-and-down circulation extends all the way to the star’s core. Without a tachocline, scientists aren’t sure how these stars produce their magnetic fields. Reinhold and his coauthor Ansgar Reiners say that applying their technique to the Kepler archive might yield clues to how important differential rotation is in generating stellar magnetic fields.
Understanding stellar activity could also affect our hopes for life in the galaxy: M dwarfs are prime candidates for detecting planets with liquid surface water, but magnetic activity could render them uninhabitable.
References
Reinhold, T. & Reiners, A., 2013. “A fast and reliable method to measure stellar differential rotation from photometric data.”
http://arxiv.org/abs/1306.2176
 2
2
Comments
Cassiano Porto
July 4, 2013 at 2:03 pm
This is a very interesting study! Mark Zastrow made an excellent article explaining it to non-physicists like me. Thanks!
You must be logged in to post a comment.
Robert L. Oldershaw
July 5, 2013 at 3:35 pm
For an interesting comparison between the spin-flipping observed in atoms and the magnetic field flipping seen in stellar systems like Tau Boo, see:
http://www3.amherst.edu/~rloldershaw
New Developments #11 "Magnetic Cycles In Stars and Electron Spin Transitions In Atoms".
Robert L. Oldershaw
Discrete Scale Relativity/Fractal Cosmology
You must be logged in to post a comment.
You must be logged in to post a comment.