Linearity — a measure of how a detector accumulates light — is important for getting the most from your astro-images, and it's not nearly as complicated as it sounds.
Unmanipulated data from a CCD or CMOS camera (this includes DSLRs) are typically linear (or nearly linear) in nature. It’s important that many of our image enhancements take place while the data is still linear, and it’s really important for the scientific community that the data stays linear to be of many kinds (but not all kinds) of scientific value. So what does this mean: the data is linear?
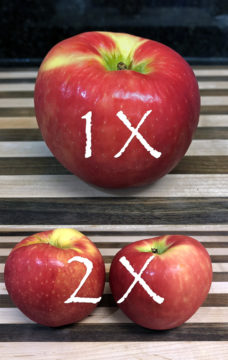
Richard S. Wright, Jr.
Time for a brief math lesson. Fear not, I assure you, you’re up to the task. I saw a meme recently on Facebook, “Come on people… when was the last time you actually used algebra in your real daily life?"
Every. Freaking. Day.
It’s not that hard or scary folks, it’s quite simple. Here’s a real-world example: If you normally buy two apples, and your spouse asks you to buy twice as many apples this time, how many apples do you buy?
Here’s another one: If you eat an apple a day, how many apples will you eat in 7 days?
Let’s make it really hard! What if you eat two apples a day for 7 days?
Congratulations, you’ve just done algebra. Not only that, you easily understand all the math you need to comprehend what people are talking about when discussing linear data. Okay, I might be stretching the definition of algebra slightly, but hey, solve for X, solve for apples… same difference! Don’t be afraid of the big math words, you’ve got this.
The main job of a camera sensor is to count photons of light. If 10 photons fall on a pixel, In a perfect world, the readout for that pixel would be 10. Unfortunately, there is some light loss due to a measurement called “quantum efficiency” (QE) that determines how effective the chip is at counting photons. If the QE is only 50%, then the chip only counts half of the photons that reach it. Some really high-end chips have a QE around 95%, but most amateur astrophotography cameras are in the range of around 50% to 75% QE.
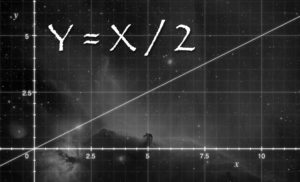
Richard S. Wright, Jr.
One of the principle advantages of electronic sensors over chemical films of yesteryear is that they record light linearly (and are many times more sensitive to light than most film). For example, if you dump twice as much light into a sensor, you get twice as much signal (even when accounting for the loss due to QE). This is a linear relationship. Ta-da! The same was not true of film, which suffered from “reciprocity failure” where more and more light just didn’t seem to nudge things any further along on the film. So for low-light, long-exposure photography of any kind, silicon wins hands down.
So why is linearity important? Well a number of reasons. First, it means you can expose longer and accumulate more signal. Expose twice as long, get twice the signal. That alone is a pretty big deal that we often take for granted today. Second, the data is more useful for certain types of science. Let’s say you’ve recorded a supernova in your image. You can measure the photon counts of the pixel the supernova was recorded on and compare it to a nearby star of a known brightness. If a star’s brightness is 10 apples, and the supernova is 100 apples, then you know the supernova is 10 times as bright as the star. Oops . . . I mean ADUs (analog-to-digital units), not apples. You get my drift?

Richard S. Wright, Jr.
The same goes for variable star studies. Many stars fluctuate in their brightness and we watch them, measuring their brightness changes over time. The only way to accurately do this is to have a reference brightness for each image of the variable star, and that reference is usually nearby stars of known brightness. If our sensors aren’t linear, we can’t be sure that there is a linear scale between these two light sources in our image.
When it comes to image processing, many of the algorithms that we use to make a visually pleasing astrophoto work best when the data is still in a linear state. The linearity of your data, by the way, has absolutely nothing to do with why it may look dark, that’s a whole different topic, and I’ll talk about stretching another time. There will be more math, but I’ll see if I can’t work some apples into it.
There are a few things we need to add to this discussion. Data from the camera needs to be properly calibrated if you expect your data to be perfectly linear. You have to subtract a dark frame to remove the dark current offset and bias signal that is present in every image. You also should properly calibrate with flats to even out the effects of vignetting or other light obstructions (such as dust bunnies in your optical path).
Also, here’s a few other factoids: Most CCDs in commercially produced astronomical cameras are not linear over the entire range of signal. As they near saturation (all the apples that will fit in the pixel), they start to lose linearity. Each chip varies, but typically the linear range works up until the pixels are about two-thirds full (that is, two-thirds of the detector's full well capacity). These detectors are known as anti-blooming chips, because they include an anti-blooming gate that bleeds off photons as the pixel nears saturation.

Tom Bisque
CCDs without an anti-blooming gate are more sensitive (have higher QE) and are linear over their entire range of sensitivity all the way until they are fully saturated. They then spill that extra charge onto adjacent pixels (like the example at right). It’s the anti-blooming circuitry in most consumer CCDs that lowers the QE of the sensor and is also responsible for the non-linearity at the top of their range. So the "non-anti-blooming" CCDs are prized by the scientific community for this reason.
CMOS, the golden child of 21st-century photography, has a linearity problem, and many CMOS chips are non-linear over a larger range of brightness values than a comparable CCD. Ask the manufacturer about the linearity of their chip, or Google it before using CMOS for scientific measurements. Your chip doesn't have to be perfectly linear for scientific work, but you do need to know how large your errors may be.
Flat-field calibration frames will only work if they are linear. This means you have to subtract a dark frame from your flat-field frames for them to work properly. It's also important to make sure the ADU counts of your flat fields stay in the linear range of your sensor, and that all of the signal you want corrected is also in the linear range. Again, you should inquire with the manufacturer of your camera for the optimum range to use for your camera.
I’ll leave you with this tease for next month. Stretched data can still be linear!
 0
0









Comments
You must be logged in to post a comment.