What Magnification Is That?

How can we correlate visual magnification to our photographs?

A trigger word for me is "magnification". In particular, questions like "what's the magnification of that photograph?". For starters, I don't really think the question makes sense. It's like, "How many gallons of water are there in soup?", it sounds like there should be an easy answer, but it's an incomplete question. Nevertheless, people want to know some kind of correlation to magnification for a photograph, so here's my attempt.

My pet peeve here is in how I insist on defining magnification, and in my view, there is no such thing as magnification when it comes to a camera. I'm going to be a stickler (or curmudgeon) and define magnification as the amount an object is enlarged in comparison to how large it would look to the unaided eye at a given distance. If an object looks twice as large, it is magnified 2×. You can also make an object look twice as large just by getting closer to it, exactly by half. When it comes to terrestrial photographs, you can literally move your arm back and forth and it changes how large the object is compared to a naked-eye view of the object. You are also changing the magnification just by zooming in on the objects image on your computer screen. Can we correlate this though to magnification? Yes, but we must reframe the question while providing more information and context.

A telescope's focal length is the distance the light travels from the primary lens or mirror to where it comes to focus at the image-plane The size of the image projected there is directly proportional to the focal length of the optic. The longer the optic's focal length, the larger the image appears. It’s nice and linear, too: twice the focal length yields twice the image scale. It's the same effect as getting twice as close in the mountain photograph example above.

So an image produced by a 1,000-mm focal-length telescope will be twice as large on your camera's sensor as the image from a 500-mm telescope. 2× the magnification . . . but this has nothing to do with how large the image will be finally displayed! For visual astronomy this makes more sense because we are looking directly at the image projection. Most of us know how to compute the visual magnification of our telescope when using an eyepiece: Divide the focal length of the telescope by the focal length of the eyepiece. For example, a 1,000-mm telescope with a 20-mm eyepiece gives a relative magnification to our eye of 50× when looking through the eyepiece. When doing outreach with my local club, I will often divide the Moon's distance by the magnification and tell people they are looking at the Moon as if they were flying XX miles above the surface. Yes boys and girls, a telescope is a space ship and you can have one too.

Okay, so what is the magnification of the image projected by the telescope with no eyepiece? Well, if you put your eye at the focal plane, it turns out there is an easy answer to this as well. Your eye has a focal length of about 22 mm (give or take a few millimeters, depending on who you ask), so you can treat your eye just like it was an eyepiece. For a 1,000-mm focal length optic with no eyepiece, your view would be about 45×. Try it! Point your telescope at the Moon and see if you can spot it without an eyepiece. You sure can, but it might be tricky getting your eye just the right distance to see it focused. I discovered this by accident years ago when I realized that a very nice image of the Moon was being projected on my white t-shirt while changing eyepieces.

So, an image captured at the focal plane of this telescope is magnified 45×, right? Not so fast — you aren't putting your eye there, you are placing the camera's sensor there. That image sensor might well be 20 mm across too, so the image captured of your target is 20 mm across to start with, but when you put it on your computer screen it might appear several inches across. That's right, the raw image is magnified again when it is seen on your display device. On your phone, your target map appear 2 inches across, and on your big screen TV, the same image will appear a couple of feet wide! In these situations, how big is the object compared to when you view it naked eye? This sounds like a formidable math problem, but it actually has to do with just two things: The field of view of the target (how wide the portion of the sky was captured), and the field of view of the resulting image as it's displayed.

Let's use an image of the full Moon as an example. When you look at the Moon in the sky, we don't say it looks half an inch across. We say how wide an angle the object subtends. The full Moon is about 0.5° across.

So, how magnified is this image of the Moon to the right, then? In the end, the telescope focal length and camera chip size determine the field of view captured (bear in mind, you could also crop the image down a bit as I've done here). All we need to know is the ratio of the actual naked-eye visual angle (0.5°), compared to the visual angle the image on the screen represents.

The visual angle of any object, be it the Moon in the sky, or a photograph on a computer monitor, at a given distance is given by this formula:

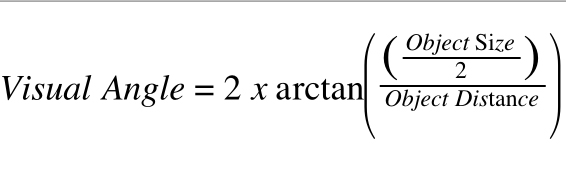
Size and distance must be the same units. They can be inches or miles because there is a nice linear relationship between size and distance. Twice as close is always twice as large—doesn't matter if it's inches, miles, or parsecs.

On my computer monitor as I type this, the image is 2 inches across and is 15 inches away. Plugging those values in, I get a visual angle of the Moon image as 7.6° (put your calculator in degrees mode for this unless you want to use radians for your image field-of-view computation).

The image on my screen of the Moon is 7.6°, and I divide that by the .5° the Moon appears to me in the sky, and voila, the image on my screen is about 15× normal size . . . or . . . magnified. Oh yeah! Try this with some of your favorite astro-images to amaze your friends and family!