The secret to stacking images is increasing signal rather than just increasing the number of exposures.
Last month we laid the groundwork for further discussions of noise in our astrophotos. One of the most significant sources of noise is shot noise, a type of noise inherent in all digital images. Our deep-sky images contain shot noise; calibration frames do, too. So how do we deal with it?
Why Stack Images

[credit, Richard S. Wright Jr.]
Simply taking longer exposures is tricky, due to equipment constraints, it's difficult for most mounts to keep stars on the same group of pixels for more than a few minutes. Even with great care and finely tuned gear (as well as computer-controlled autoguiding), there are practical limits that prevent us from taking a single exposure that might last for several hours to get a high enough S/N ratio for a nice clean image. Airplanes, satellites, and the weather all conspire to ruin a single hours-long exposure. Not to mention, most cameras will saturate (become all white) if exposed too long, especially from a light-polluted location.
But you don't need long exposures or fancy equipment to get more signal. We can also get more signal by combining multiple exposures, a procedure called stacking.
Stacking involves combining many short exposures. Instead of a single 60-minute exposure, we might take twelve 5-minute exposures, or thirty 2-minute exposures. If you add all the exposures together, you’d have the equivalent of 1 hour of exposure time. (Of course, it's slightly more complicated than this – you do need to calibrate individual frames, which we'll discuss later).
Typically, we do not sum (add together) images; instead, we average them. Averaging images yields the same signal-to-noise ratio as summing up properly calibrated images, but it also has the advantage of keeping the numerical values that make up the image in the same range as that reported by the camera. Essentially, it's as if the camera had taken a single image with way more signal than you would normally obtain in a single, short exposure.

Richard S. Wright Jr.
Stacking is often misunderstood, even by some very intelligent and gifted astrophotographers. This is due to a common misconception about math and the physical world:
Math is a tool that can describe how the world works. However, the world does not obey “the math.” Math serves physics, not the other way around.
The reason I want you to understand this is because I am about to tell you something that appears to contradict all the graphs you’ve ever seen about stacking. You see, the signal-to-noise ratio does not actually go up because of the number of exposures in a graph, but rather because the number of exposures is increasing the signal faster than it's increasing the noise.
This concept is very important to wrap your head around, because there’s a lot of talk about diminishing returns for the number of images that you stack. Should you stop at 12 images, 24, 240? There's no answer to this question because it's an incomplete question, and those who would give you a simple number are fundamentally missing how this stuff works.
Typically, those who would just quote a number will show a graph such as the one below, saying it shows how the noise decreases with the number of exposures. To the casual observer, then, it's pretty obvious that after about 16 or so exposures, that line is not moving nearly as quickly towards the X axis, and that might be a good time to give up and start on a new target.
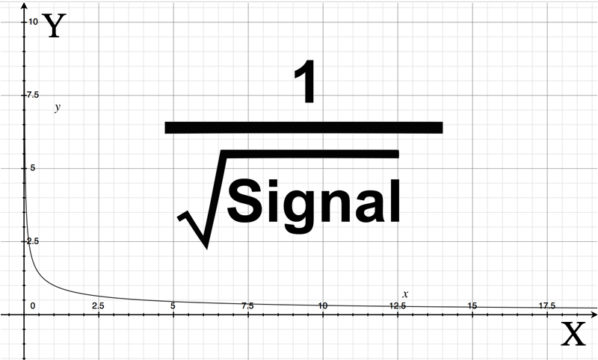
Richard S. Wright Jr.
The problem is this graph isn't showing how shot noise decreases with the number of exposures, it's showing how noise decreases with accumulated signal. In some ways it's the same thing. But despite the intuition from this graph that 16 to 20 exposures is about as good as you can do, there's a huge difference between sixteen 1-minute exposures and sixteen 5-minute exposures. (Try it if you don't believe me!)
The physics isn’t about exposure time, it’s actually about how much light you collect . . . how much signal! A question about diminishing returns can only really be answered in the context of how much signal you need before noise becomes negligible. The answer depends on your optic, your camera, and the target you’re shooting.

Richard S. Wright Jr.
I can tell you that with one of my cameras on an f/3 telescope, I can expose the Andromeda galaxy for two minutes and obtain an image where the core, as well as its immediate vicinity, are as smooth as glass. Farther from the core, though, the image appears dimmer. Where there's lower signal, the image appears noisier. Those outer dust bands and spiral arms need a lot of integration time to accumulate enough light to drown out the noise. So, how many images do I take before I start seeing negligible returns? Well, near the core the answer seems to be exactly one — not 16. One image captures tons of signal and negligible noise.
What about the galaxy's outer arms? Well, I promise sixteen 2-minute exposures is going to look considerably cleaner than sixteen 1-minute exposures; exactly 25% more noise-free, if you do the math. Is 25% enough? For a bright target like Andromeda, it might well be. If it's a dim target with very little signal, this might fall very short. Rules of thumb are so comfortable when we are getting started, but at some point you need to start to learn how to apply the core principles to your gear, and your imaging targets. In terms of signal . . . more is always better!
So why not stack 3,600 one-second images? Two reasons: read noise and dynamic range. Simply put, to get the best results you need to expose long enough to get your signal out of the gutter of your histogram.
The graph above does, however, work well when considering the number of exposures required to stack your darks and flats. Perhaps you already understand enough to guess why. If not, stay tuned . . .
 2
2









Comments
Martian-Bachelor
May 31, 2018 at 1:52 pm
Ha! I can see in your side-by-side comparison photos that you didn't use your circular aperture mask for those. Now I'm going to be seeing those lens aperture blade star spikes everywhere... thanks!
Kidding aside, people often want to know what their limiting magnitude (LM) is. I'd like to see someone construct a graph showing LM versus either the number of images stacked or the total exposure time (maybe on a logarithmic scale). This could almost be done with very short focal length lenses (around "normal"), relatively short exposures, and regular star maps. I.e., using stars not any fainter than, say, the SAO catalog, just to make it tractable.
Does the LM keep getting fainter and fainter, or does it start to roll over and look like it's going to level off at some point? I've only played around with stacking a little, so I have no idea what the result would be. But the idea of being able to reach 25th magnitude objects with my 200mm f/2.8 lens if I could just expose enough 30 second frames seems preposterous.
And damn all the airplanes and satellites!
You must be logged in to post a comment.
Richard S. Wright Jr.Post Author
June 9, 2018 at 11:09 am
Hi, and yes those images were pre-aperture mask days
This is a great idea for a followup blog sometime down the road. Separating a faint star from the skyglow is one challenge, but also the read and shot noise. Stacking will help with both of those, but at some point it’s going to be “practically” impossible to do better. Stacking away read noise completely is for all intents and purposes “prohibitive”, and so the limiting magnitude is also a function of your cameras read noise. Yep… great topic idea… for sometime!
You must be logged in to post a comment.
You must be logged in to post a comment.