A slow, relentless rhythm, known as the saros cycle, is hidden away in the movements of the Moon and Sun. How does it foretell eclipses — and how could Babylonians discover its existence long before modern science and technology?
With agonizing care, the astronomer worked through the data one more time. Yes, there it was: an unmistakable pattern, locked away in the figures inscribed on the clay tablets. Dizzily, the astronomer walked to the window and gazed out at the sprawl of Babylon. A red sun and thin crescent moon hung low over the walls of the city. Got you, he thought.
We do not know the name of the astronomer. Nor do we know precisely when, where, or how the discovery was made. But we do know that, 2½ millennia ago, a Babylonian astronomer realized that eclipses come in cycles that are 6,585 days long. Today, Babylon — once the largest city in the world — lies in ruins. But the eclipse cycles, which we call the saros, continue to beat their slow, relentless rhythm.
Let's look at a map of last summer's Great American Eclipse, which took place on August 21, 2017. The path of totality, indicated by the narrow red line, stretched 8,000 miles across the globe, from the Pacific to the Atlantic Oceans. The lighter, orange-shaded areas show the area where a partial eclipse was visible.
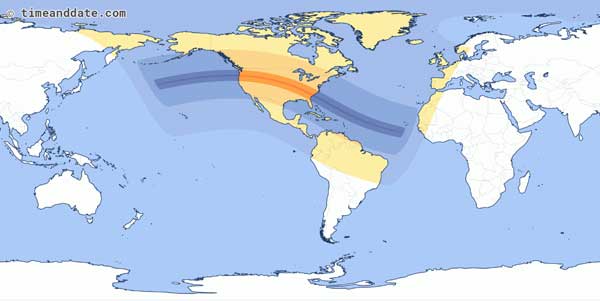
timeanddate.com
Now let's wind the clock back 6,585 days to August 11, 1999. Sure enough, on this day there was another solar eclipse. Some S&T readers may recall it: a high-profile total eclipse across the UK, Europe, the Middle East, and southern Asia. If we look at the map of this eclipse, we can see that the shape of the path of totality, plus the areas that experienced a partial eclipse, are almost identical to the Great American Eclipse.
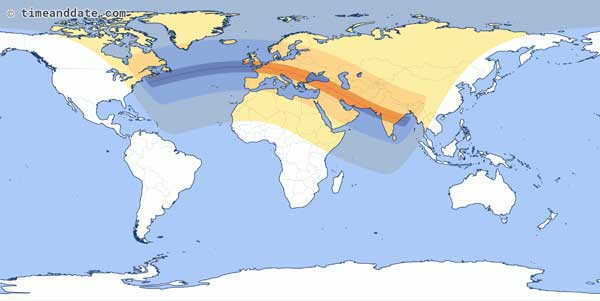
timeanddate.com
There are important differences between the maps. The first, and most obvious, is that the 2017 eclipse took place to the west of the 1999 eclipse: the path of totality is shifted ⅓ of the way around the globe. This is because the saros cycle is actually 6,585.32 days long — that extra 0.32 of a day means that the earth sneaks in an extra ⅓ of a spin on its axis.
The second difference is that the Great American Eclipse took place very slightly to the south of the 1999 event. The reason for this is that the saros cycle is not perfect. The figure of 6,585.32 days is equivalent to 223 synodic months of 29.5306 days each. (A synodic month is the period of time from one new moon to the next.)
But a solar eclipse requires more than a new Moon. It also requires the Moon to be aligned with Sun. This doesn't happen every month, because the Moon's orbit is tilted. The period of time needed for the apparent path of the Sun to carry it from the Moon's ascending node to its descending node and back again is called an eclipse year, and lasts 346.6201 days. (The nodes are the points where the moon crosses the plane of the earth's orbit.) Nineteen eclipse years is equivalent to 6,585.78 days, which is almost — but not quite — a perfect match with 223 synodic months.
There is one more thing to consider: the distance of the Moon from Earth. The Moon's orbit is elliptical, and the time it takes for the Moon to go from perigee (its closest point to Earth) to apogee (its furthest point) and back again is called an anomalistic month, whih lasts 27.55455 days. Sum 239 anomalistic months and the total comes to 6,585.54 days — just a few hours longer than 223 synodic months, and a few hours shorter than 19 eclipse years. These few hours account for the small differences in successive eclipses in a saros cycle.
Aside from that, however, the eclipses of August 21, 2017, and August 11, 1999, are essentially the same. For example, the U.S. city of Salem, Oregon, is in more or less the same place on the path of totality as the UK city of Truro, Cornwall. If we look at the animation of the eclipse for each city, we can see that, separated by 18 years, 11 days, and 8 hours, the two eclipses in Salem and Truro are almost identical.
This all leads to a big question. Since successive eclipses in a saros cycle take place in different parts of the globe, how did the Babylonians, who didn't travel much beyond the region that is modern-day Iraq, discover the pattern? The answer is that saros cycles apply to lunar eclipses as well as solar eclipses — and a lunar eclipse can be observed from across half the globe. The Babylonians' clay tablets contained a record of half of all the lunar eclipses that occurred.
Again, we can check the animations to demonstrate that successive lunar eclipses in a saros cycle are pretty much the same. Let's compare the forthcoming total lunar eclipse on January 31st (which comes 163 days after the Great American Eclipse) with the total lunar eclipse of January 21, 2000, (which came 163 days after the August 1999 solar eclipse).
Read more about the upcoming lunar eclipse here.
Solar eclipses have provided scientists with some glorious "teachable moments," from the discovery of helium in 1868 to a proof of general relativity in 1919. And yet it is lunar eclipses that gave astronomers one of their earliest opportunities to unlock one of nature's secrets and — who knows? — perhaps to look up at the Moon and Sun and think: got you.
Further Reading
Sky & Telescope's preview of this month's total lunar eclipse
Chapter 1 of David Leverington's Babylon to Voyager and beyond: A history of planetary astronomy (Cambridge University Press, 2003) includes an overview of Babylonian astronomy.
In chapter 17 of Totality: Eclipses of the Sun (Oxford University Press, 2011), Mark Littmann, Fred Espenak and Ken Willcox trace the history of the saros 136 cycle of eclipses, which includes the famous Einstein eclipse of 1919.
 1
1
Comments
Rod
January 25, 2018 at 11:37 am
Good report. Establishing secure, anchored dates in Babylonian and Mesopotamian ancient history is important and the saros cycle helps when examining ancient records of solar and lunar eclipses. If any folks have encountered flat earth (FE) astronomy on the Internet today (livescience and phys.org recently reported some info on the topic), flat earth astronomy teaches the Sun is 3,000 miles away (FES Sun wiki) and the Moon is 3,409 miles away (SmokeScreen Design wiki using parallax and non-spherical earth trigonometry with their baseline). In FE astronomy there would be no solar eclipses or saros cycle (distance to the Moon and Sun) as we see in astronomy (also no elliptical orbits). Looking at the saros cycle, if we extrapolate back millions and several billion years, the lunar period and distance of the Moon from Earth changes too along with Earth's L.O.D. In the giant impact model, the Moon forms about 15,000 miles away from Earth and then slowly expands outward to its present position (roughly 3-60 earth radii change in distance).
You must be logged in to post a comment.
You must be logged in to post a comment.