Should you use light-years or parsecs for astronomical distance?

By: Alan MacRobert July 21, 2006 1

You give astronomical distances beyond the solar system in light-years, but professional astronomy papers use parsecs. Which is preferable?

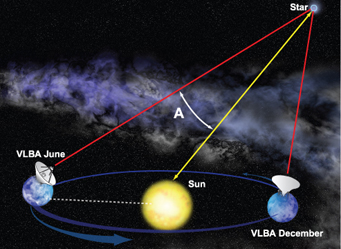
Light-years, no question! Here’s how I see it. The parsec (which equals 3.26 light-years) is defined as the distance at which a star will show an annual parallax of one arcsecond. This means it is based on two arbitrary quantities: the radius of Earth’s orbit, which was a random accident of how the solar system fell together, and the definition of the arcsecond — an even more arbitrary unit that stems from the ancient Babylonians’ base-60 style of arithmetic, along with their notion that the circle should be divided into 360 degrees because there “ought to be” 360 days in a year. The light-year, by contrast, is based on only one arbitrary value (Earth’s orbital period) and on a fundamental constant of nature: c, the speed of light.

Moreover, as a practical matter, few distances in modern astronomy are directly measured by the parallax method anymore. However, it’s often important in modern astrophysics to know the light-crossing time of a given distance — and if the distance is given in light-years, there you are.

— Alan MacRobert

About Alan MacRobert

Alan M. MacRobert became an avid Sky & Telescope subscriber in 1966 at age 14, joined the editorial staff in 1982, and is now a senior contributing editor, semi-retired. He played a role in practically every part of the magazine and the company's other products for more than a generation, both on the amateur-observing side and the science-reporting side. In 1994 a book collection of his observing how-tos and telescopic sky tours was published as Star Hopping for Backyard Astronomers. He has produced This Week's Sky at a Glance online every week since 1989.

Comments

kazvorpal

October 19, 2018 at 9:24 pm

One significant flaw in this argument is that base 60 is slightly LESS "arbitrary" (as you're using that word) than base 10. There is nothing scientific, nor objective, about our base 10 system. We use it because we're monkeys that need to learn to count on our fingers, not because it's in any other way effective.

Base 60 is much more objective and potentially useful as a radix.

The most objective would be binary, followed by any power of 2. We'd be better off with base 8 or base 16 than with base 10. But base 60 comes in well before base 10 on the list of potentially useful systems.

You must be logged in to post a comment.