Once you hold the golden keys of right ascension and declination, finding your way around the sky is almost as easy as finding your way around town.
Stellarium
Sooner or later every novice skywatcher runs into the terms RA and Dec., short for right ascension and declination. When I got started in astronomy at age 11, they were a little scary. Then I realized they were just numbers like latitude and longitude, except applied to the stars.
Latitude & Longitude
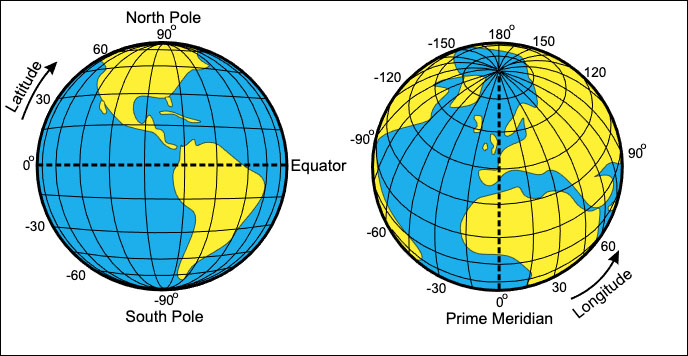
To find anyplace on the globe of Earth, you only need to know its latitude, the distance in degrees north or south of the equator, and longitude, the distance in degrees east or west of the prime meridian. The prime meridian is an imaginary line that runs through the Royal Observatory in Greenwich, United Kingdom, and extends to the North and South Poles. It defines the the zero (0°) longitude line just as the equator defines the 0° latitude line.
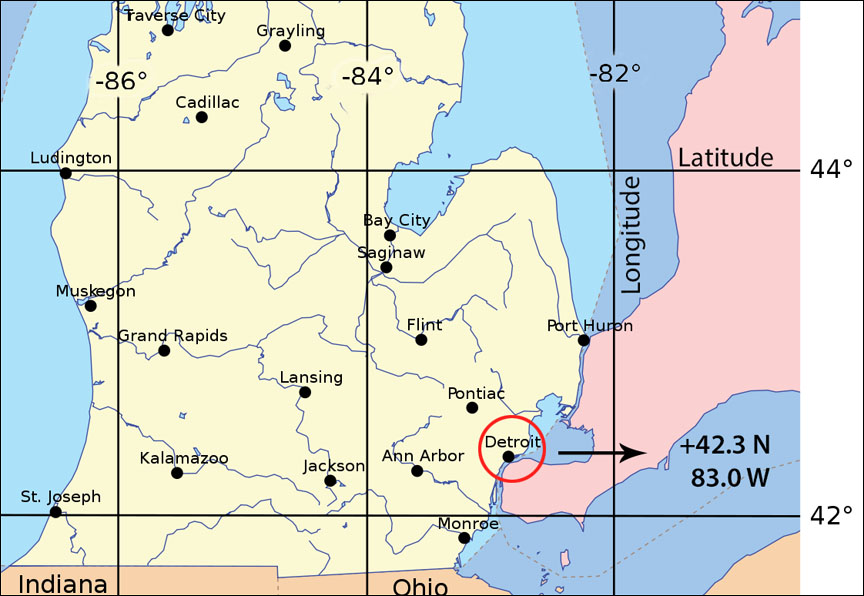
Each city has a unique latitude and longitude. Take Tuscaloosa, Alabama, for example, which is located at latitude +33.2° north, longitude 87.6° west. Or Wonglepong, Australia, situated along that continent's east coast at –27.0° south, 153.2° east. A negative sign in front of the latitude indicates south and a positive sign north. Every location, whether it be a city, airport, or even your own home or apartment building lies somewhere on the worldwide coordinate grid (below), its location fixed by two numbers.
CC0 1.0
Each degree of latitude is equal to about 111 kilometers on Earth's surface. For precision we break down degrees into either fractions of a degree or divisions called minutes and seconds of arc. There are 60 minutes in one degree and 60 seconds in one minute. Tuscaloosa's precise location is +33° 12′ (minutes) 35″ (seconds) north, 87° 34′ 9″ west. You can convert fractions of degrees into minutes and seconds here.
CC 3.0 / Wikipedia
Right Ascension & Declination
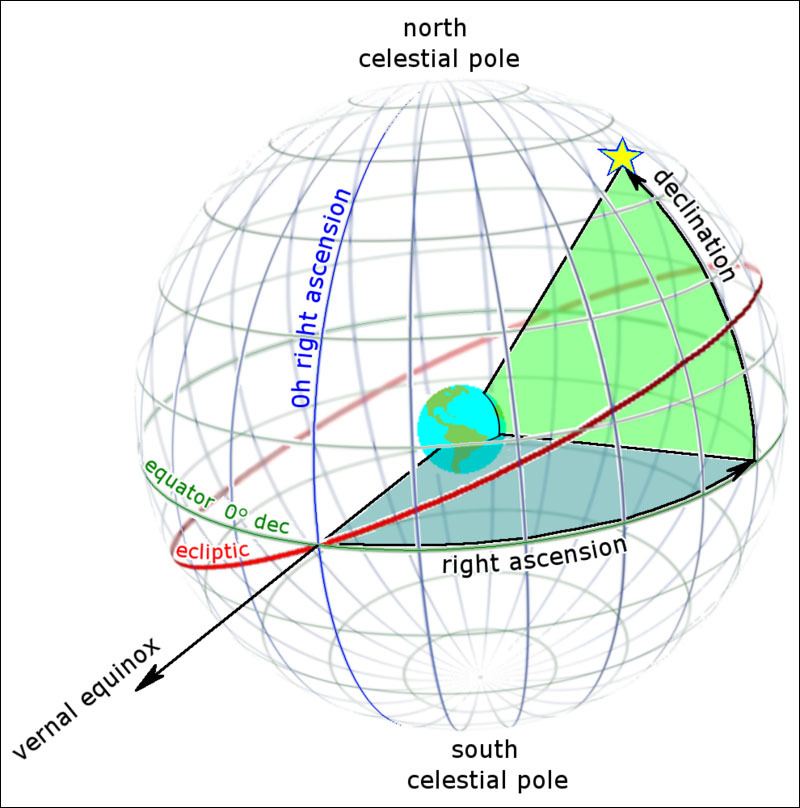
Like cities, every object in the sky has two numbers that fix its location called right ascension and declination, more generally referred to as the object's celestial coordinates. Declination corresponds to latitude and right ascension to longitude. There are no roads in the sky, so knowing an object's coordinates is crucial to finding it in your telescope.
Let's use our imaginations and picture the latitude–longitude grid on the planet as the surface of a flexible, transparent soccer ball. If you could pump the ball up into a gigantic sphere centered on the Earth, you'd look up and see lines of latitude and longitude imprinted on the sky. The equator, which marks the 0° latitude line, now circles the sky as the celestial equator, while the north and south celestial poles hover over either end of the planet's polar axes.
Viewed from Earth's equator, the celestial equator begins at the eastern horizon, passes directly overhead and drops down to the western horizon. Since we're inside a sphere, it would continue around the backside of the Earth as well.
Tom Ruen / CC BY-SA 3.0
From mid-latitudes, the celestial equator stands midway between the horizon and overhead point, while from the poles the celestial equator encircles the horizon. Anything north of the celestial equator has a northerly declination, marked with a positive sign. Anything south of the equator has a negative declination written with a negative sign. For instance, Vega's declination is +38° 47′ 1″, while Alpha Centauri's is –60° 50′ 2″. One star is north of the celestial equator and the other south. Can you guess the declination of the north celestial pole? If you said +90°, you're already getting the hang of this.
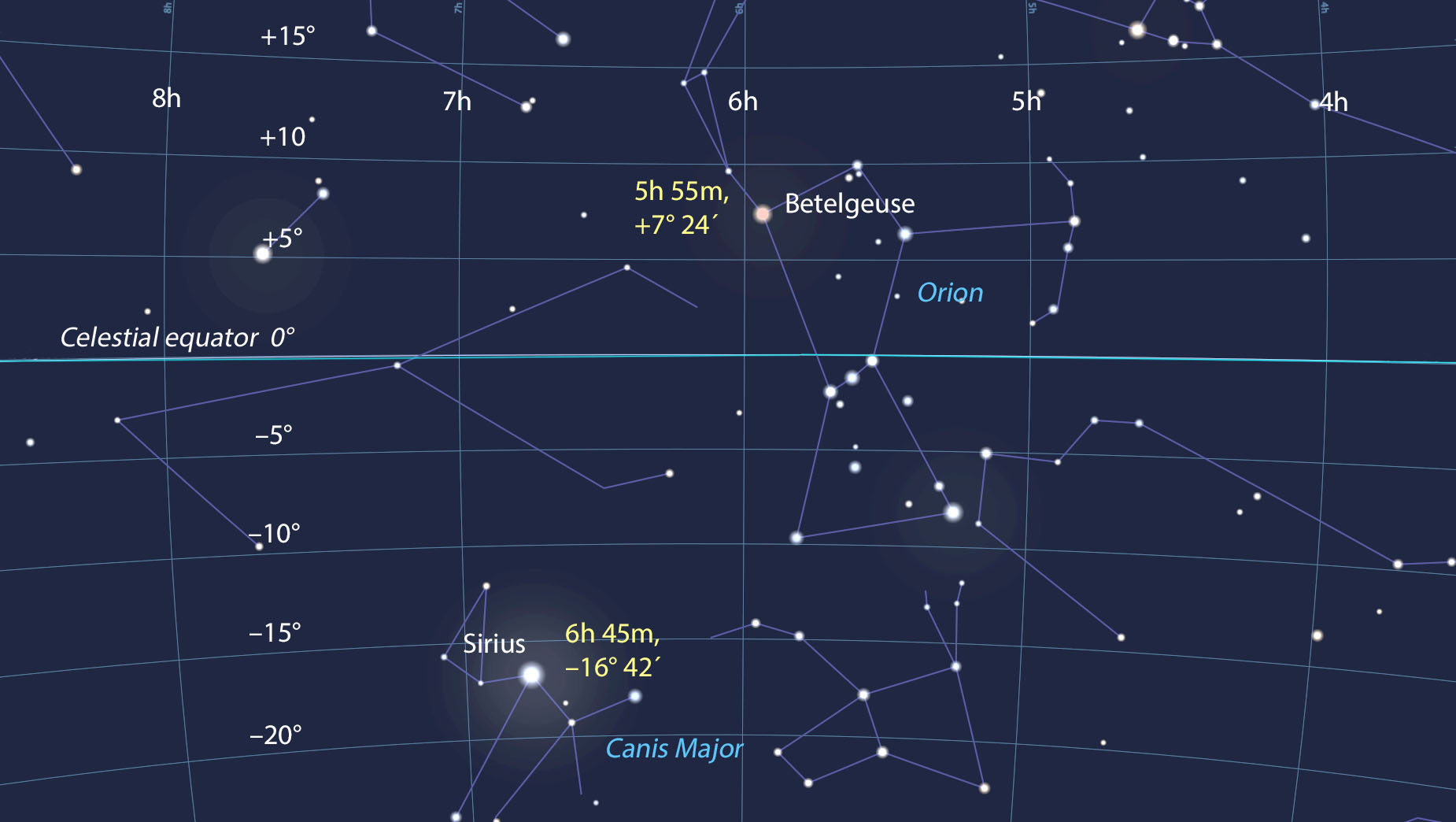
Stellarium
While we use a physical location on Earth as our reference for longitude, what reference do we use for right ascension? Where is the 0° mark in the sky separating east from west? Astronomers use the spot the Sun arrives at on the first day of spring, called the vernal equinox. Presently, it's located in the constellation of Pisces, the Fish. The sky can be treated as a clock, since it wheels by as Earth rotates, so the zero point of right ascension is called "0h" for "zero hours." Unlike longitude, right ascension is measured in just one direction — east. Because there are 24 hours in a day, each hour of right ascension measured along the equator equals 1/24th of a circle (360° divided by 24) or 15°. That's a little more than one-half the width of the W-shaped constellation Cassiopeia.
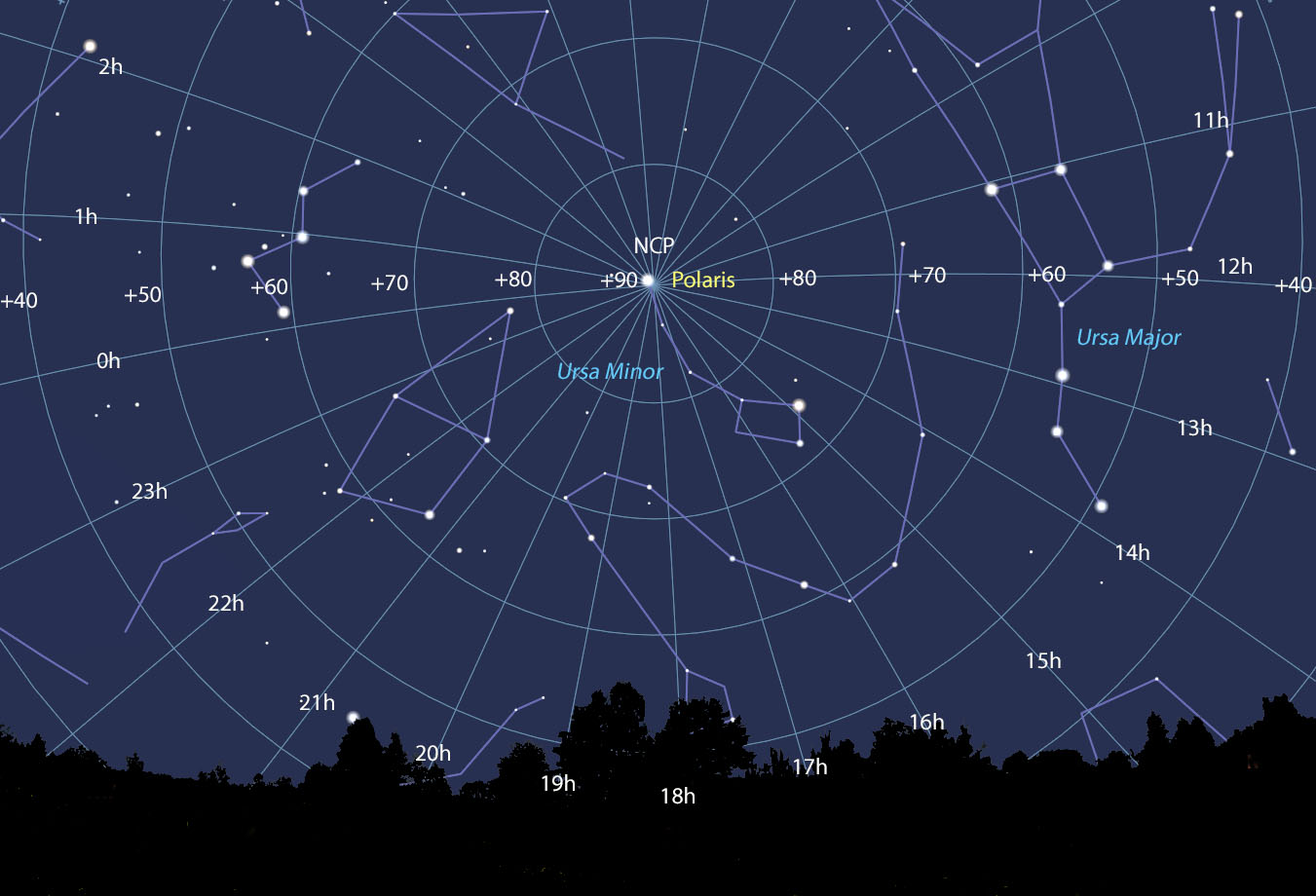
Stellarium
In keeping with right ascension's time theme, hours are subdivided into minutes and seconds, and are even written out as minutes (m) and seconds (s). Let take the North Star for example. Polaris is located at RA 2h 41m 39s, Dec. +89° 15′ 51″. Because the stars circle about the sky every 24 hours, right ascension or RA ranges from 0h to 24h. The star 29 Piscium, located immediately east of the equinox point is very close to 0h with an RA of 0h 01m 49s, while its neighbor, Omega (ω) Piscium, located just west of the equinox point, has an RA of 23h 59m 19s.
Unlike Earth coordinates, celestial coordinates change due to the slow wobble of Earth's axis called precession. Precession causes the equinox points to drift westward at a rate of 50.3 arcseconds annually. As the equinox shifts, it drags the coordinate grid with it. That's why star catalogs and software programs have to be updated regularly to the latest "epoch." This is done every 50 years. Most catalogs and software currently use Epoch J2000.0 coordinates (for the year 2000). The next major update will happen in 2050.
Learning RA and Dec. provides you with a golden key to unlock the position of any object in the night sky. Before computer software effortlessly plotted the paths of newly discovered comets and fast-moving asteroids, I couldn't wait to get my hands on their coordinates. I'd hand-plot the positions on a paper star atlas, then swing my scope to the spot, and thrill when I found it on my own.
RA and Dec. also come in super-handy if you have a Go To telescope and a new comet or nova is discovered. Just input its coordinates, hit enter, and you're there. If you hear of a new comet or fast-moving asteroid, a quick check of its changing coordinates will tell you not only where it is but where it's headed, so you can plan the best time to see it.
I made friends with right ascension and declination long ago. Knowing I could drive anywhere on its invisible roadways helped me, and it'll help you too become more familiar with the night sky.
 21
21









Comments
Rod
February 26, 2019 at 4:56 pm
Good review and I enjoy RA and Dec. Much of my observing is with a Telrad. You can convert RA and Dec. by coordinate transformation (Jean Meeus Astronomical Algorithms) to your geographic location and find the altitude and azimuth of the target for viewing along with transit time, etc. I hear this works very well on *round* planet Earth. It does for me 🙂
You must be logged in to post a comment.
stewshou
March 4, 2019 at 3:27 pm
Bob King said:
I'd hand-plot the positions on a paper star atlas, then swing my scope to the spot, and thrill when I found it on my own.
I don't know how to take this step with my Dobsonian. Do I need some add on protractor etc? How do I find the vernal eqinox? How do I go to a specific RA Dec without a system to show RA Dec?
Not much sky watching this winter.
Stew Shouldice
You must be logged in to post a comment.
Bob KingPost Author
March 4, 2019 at 3:49 pm
Hi Stew,
I also use a Dob and have for many years. You don't need to know where the vernal equinox is if you're hand-plotting. You get the specific RA and Dec. of what it is you want to look at. If it's a bright star, then that's easy, you look to see if that star is up in the sky at the time you want to view it. You can do that by using a planisphere (star-wheel) or a free software planetarium program like Stellarium. If you're looking for a fainter object, you'll need a star atlas. Star atlases will always shows right ascension along the bottom and declination along the side. You locate a specific object by interpolating between those numbers. If you're looking for a new comet or variable NOT on an atlas, then you hand-plot its RA and DEC. right on the chart using a straight-edge or protractor, what have you. Larger atlases come with their own separate fine-gradation grids you can place over the page to really nail the position down. Does this help?
You must be logged in to post a comment.
sunwukong
March 12, 2021 at 2:07 pm
Can someone show me the formula to resolve altitude and azimuth of polaris using observer latitude, longitude, elevation above sea level, UT? It is interesting that Jean Meeus Astronomical Algorithms does not even have an index entry for polaris., The routines in basic for JD, F, GMST give proper results, the routines altaz.bas and altaz2.bas do not.
You must be logged in to post a comment.
Anthony Barreiro
February 26, 2019 at 7:02 pm
Bob, this explanation would fit nicely in the first chapter of your next book!
Lately I've been figuring out how to use the northern circumpolar stars and the Sun's approximate right ascension to tell time at night.
Here are the bright circumpolar stars that happen to lie close to an exact hour of right ascension:
Beta Cassiopeiae 0 h
Gamma Cas 1 h
Epsilon Cas 2 h
Alpha and Beta Ursa Majoris (Dubhe and Merak, the pointer stars) 11 h
Gamma UMa 12 h
Epsilon UMa 13 h
Beta Ursa Minoris (Kochab, the brightest star in the bowl of the little dipper) 15 h
Gamma Draconis (Eltanin, the brightest star in the head of the dragon) 18 h
Put Polaris at the middle of your imaginary clock face, find whichever of these stars are visible, and interpolate the rest of the clock. Now use the seasons or the Sun's current astrological sign* to figure out the Sun's approximate right ascension.
The Sun is at 0 hours RA at the March equinox, 6 hours at the June solstice, 12 hours at the September equinox, and 18 hours at the December solstice. Figure out how far we are between an equinox and a solstice and interpolate. Astrological signs are easier, because every astrological sign is about two hours of right ascension wide, starting with 0 h at the first point of Aries, 2 h at the start of Taurus, etc. (the signs follow ecliptic rather than equatorial coordinates, so they don't match up exactly, but close enough for this purpose).
The next step is to deduce the angle between the Sun and a convenient circumpolar star, and finally to figure out where the Sun's right ascension is on your circumpolar clock. Imagine the Sun moving below the horizon from your western horizon toward the eastern horizon, and that allows you to "see" where the Sun is at any given moment from sunset to midnight and from midnight to sunrise.
The Sun is currently about one week into the sign of Pisces, or three weeks before the March equinox, so the Sun's right ascension would be about 22 hours 30 minutes (according to theskylive.com, the Sun's current RA is 22 h 38 m). In other words, the Sun is about 30 minutes west of being opposite Dubhe and Merak. So if it's nighttime and Dubhe and Merak are east of the meridian, the Sun is west of the meridian, i.e. it's before midnight. When Dubhe and Merak are transiting the meridian it's 30 minutes after midnight, and when Dubhe and Merak are west of the meridian the Sun is east of the meridian, i.e. it's after midnight. By estimating the angle between the pointer stars and the meridian (and adding the equation of time), I find I can estimate the time to within 15 or 30 minutes.
Anyway, it's a bit of fun that needs neither optical aid nor an especially dark sky.
* No further endorsement of the validity of astrology is hereby expressed or implied.
You must be logged in to post a comment.
Anthony Barreiro
February 27, 2019 at 5:43 pm
I made a mistake: in order to get the most accurate estimate of clock time, you need to *subtract* (not add) the equation of time to your local solar time. The current equation of time is (-12 minutes 45 seconds), so subtracting a negative number means that clock time is about 13 minutes later than local solar time.
You also need to correct for your longitude east or west of your standard time zone's central meridian. For each degree east of your central meridian your clock time is four minutes earlier than mean solar time; for each degree west of your central meridian your clock time is four minutes later than mean solar time. Here in San Francisco we are 2 degrees 26 arcminutes west of the central meridian, which means our clock time is an additional ten minutes later than mean solar time.
It's easy to go down a rabbit hole with timekeeping. But it's fun.
Also, the genitive cases of Ursa Major and Ursa Minor are Ursae Majoris and Ursae Minoris.
You must be logged in to post a comment.
Bob KingPost Author
March 4, 2019 at 3:43 pm
Thanks, Anthony! I like your stellar shortcuts to the hours 🙂
You must be logged in to post a comment.
Anthony Barreiro
March 9, 2019 at 10:17 pm
🙂
You must be logged in to post a comment.
Ugochuks
September 20, 2019 at 11:55 am
Please sir can you explain to me how I can convert RA in degree minute second to arcsecond
You must be logged in to post a comment.
Bob KingPost Author
September 20, 2019 at 2:45 pm
Ugochuks,
You can convert R.A. to degrees by using this calculator (https://www.swift.psu.edu/secure/toop/convert.php)/ Or you can do it manually by remembering that each hour of right ascension equals 15°.
You must be logged in to post a comment.
wkhan69
October 15, 2019 at 2:06 am
Hi Bob,
I believe I've got the general gist of what these location coordinate parameters mean (RA & dec). But, when I think about this a bit deeper, I start to miss something. Let's just look at my "Right Ascension" problem.
I understand that Right Ascension is a longitude-like celestial coordinate that varies from 0-24hrs, taken from a reference point of the vernal equinox. More specifically, for star maps that are based on the epoch 2000.0, this specifically means when the vernal equinox occurred in the year 2000. Even more specifically, the vernal equinox is a specific time and date, and location of the exact point in time, when sunrise occurred, of when the day and night were exactly equal in length. Here's question #1:
1) If the Right Ascension is referenced from "Vernal Equinox" position "0hr", in the year 2000, then why does nobody ever talk about the physical location? ie: if the right ascension (sunrise of the vernal equinox) occurred in the year 2000 in a particular city, or longitude, why doesn't anyone ever mention that. ie: (just an example) Right Ascension is always measured from longitude -80deg (close to Miami, Florida, USA), as this was a city the vernal equinox occurred in the year 2000?
2) If the star maps do not change much within a period of a few decades, (eg: take for example, the right ascension and declination of the sirius star is pretty much the same in 2019 as it was in the epoch 2000, or 1990 for that matter), then these RA and dec values should not change much within a decade or so. Ipso facto, we can deduce that the sunrise time for the vernal equinox should not change very much from year to year. ie: Since RA is measured from a reference based on the sunrise of the vernal equinox in the year 2000, then the sunrise of the vernal equinox in the year 2019 should not be very much different (assuming RA is the same today as it was in 2000). But it isn't!!! If you track the sunrise of the vernal equinox from year to year, it varies a lot! I am obviously missing something... it's driving me nuts.
You must be logged in to post a comment.
Bob KingPost Author
October 15, 2019 at 4:00 pm
Dear wkhan,
Great questions! The vernal equinox occurs exactly when the center of the sun crosses the celestial equator moving north. That spot is in Pisces at the moment and very slowly moving to the west due to precession. The event is completely independent of any clock (or sunrise time) on Earth. It is a place Earth arrives at in its orbit.
If the moment of equinox occurs at 10 a.m. on the East Coast, it happens at 7 a.m. on the West. The date of the equinox changes — it can either be March 19, 20 or 21 — due to your location (if it happens on March 21 at 1 a.m. in New York, it occurs at 11 p.m. on March 20 in Denver, located two time zones west.) and the fact that the Earth does not revolve around the sun in an even number of days but rather 365 1/4 days. So each year, the time of equinox slips backward 1/4 day (6 hours) until we correct it with a leap year every four years. Other refinements keep the day from drifting from the March 19-21 slot. Let me know if this helps.
You must be logged in to post a comment.
wkhan69
October 15, 2019 at 6:45 pm
Hi Bob,
Thanks for your quick reply. I am determined to defeat this problem! For question 1, a lot of star maps are based on the epoch J2000.0. So, this time should be a specific occurrence, for all references to go by. I also understand that the earth is always spinning, and time and date are always relative to where you are in the globe, but this exact point of sunrise, when day and night are equal, in the year 2000, should be a specific location -we can even disregard what time this occurred for now. From that location, all "longitudinal" references are based. Hence, we get the 24hr RA reference for all stars because it's really referenced from a *physical longitudinal location*. The question becomes, how come no one says for epoch 2000 (year 2000), RA is referenced from longitude X, near such and such city? When people talk about RA, they just refer to vernal equinox, but really it would be much more helpful to say even a longitude coordinate (for year 2000). Can you comment on this?
You must be logged in to post a comment.
Ugochuks
March 1, 2020 at 12:20 am
Thank you so much for your help sir
You must be logged in to post a comment.
Luvlivemusic
March 11, 2019 at 11:21 pm
Hey Bob!
great article! But I'm not a young man anymore and it's a bit tough to get some things through my feeble brain. Am I correct in understanding the the difference between finding Cassiopeia and Ursa Major is just the RA? As I read this they both lie at 60 degrees of Dec. but one is at 1 hour RA and the other at 12 hour of RA. Am I on the right track here? Sorry to be so daft.
Michael
You must be logged in to post a comment.
hem
October 13, 2020 at 2:10 pm
A star is observed at zenith with equatorial coordinates, a(alpha)= 3 hours 17 minutes and delta= 40 degrees. What will be the location of observer on earth?
You must be logged in to post a comment.
Bob KingPost Author
October 13, 2020 at 3:59 pm
Hi Hem,
It would be somewhere along the 40-degree circle of latitude because no time is specified.
You must be logged in to post a comment.
Camaro Wang
October 5, 2021 at 4:06 pm
Hi Bob,
Thank you for the detailed and vivid article, but as a beginner of stargazing, I am still wondering about the specific right ascension of a star.
I can imagine that the declination of a star at any time of the day is fixed, and is the corresponding angle of the arc (of the great circle) formed by the north celestial pole and the star, but what about the right ascension. Since the earth is turning from west to east, in the Northern Hemisphere, the sky we see should be turning "anticlockwise", and if the RA is measured in the east direction, the RA of a star should decrease by 1 h after every hour (is this correct?). The problem is if we want to find a star without the help of any software, in what way can we remember the RA of a star, should that be something like "the RA of Vega is 16h at 22 o'clock"?
For example, "Polaris is located at RA 2h 41m 39s, Dec. +89° 15′ 51″.", what is the time when the RA of Polaris is "2h 41m 39s" and should this change to "2h 41m 38s" in the next second?
The last question is, how do we use our eyes to measure the declination and the right ascension of stars, or is it not measured with our eyes at all? we can quickly find the Polaris, so it should be easier to approximate the value of "90 minus declination", but how can we accurately divide the hemisphere (with the equator as the base) into 24 sections? (and would it be better if there is a reference star for measuring the RA? As it may be easier to find a familiar star than the vernal equinox)
Thank you so much!
You must be logged in to post a comment.
Bob KingPost Author
October 5, 2021 at 6:55 pm
Hi Camaro,
Fantastic questions. First, know that a star's right ascension (R.A.) and declination (Dec.) are fixed somewhat like latitude and longitude. They don't change with the ticking of the clock. If Vega's R.A. is 18h 37m and Dec. +38° 47' that's what it is. Those numbers slowly change due to Earth's precession but only after decades as far as we're concerned. Declination, as you wrote, is straightforward. As for finding Polaris its altitude is always the same as your local latitude. If you live at 38° N, then it's 38° above the northern horizon.
Because the Earth spins, which makes the sky appear to rotate, the particular R.A. that's crossing the meridian at a particular time is constantly changing. R.A. increases by about 15° per hour, equal to one hour of R.A. per hour. We use sidereal time or a clock set to sidereal time to know what R.A. is crossing at any particular time. If Vega crosses the meridian at 8 p.m. local time, the sidereal clock will read 18 hours and 37 minutes. An hour later, a star with an R.A. of 19 hours 37 minutes will cross the meridian. Two hours later, stars with R.A.s of 20 hours 37 minutes will do the same. Meanwhile, Vega will have moved about 2 hours of R.A. to the west.
Let's say you look at your sidereal clock and it reads 13 hours 7 minutes. Since you know Vega's R.A., just do the addition, and you'll know that the star will cross the meridian in 5 hours and 30 minutes.
R.A. is measured eastward from a point in Pisces where the ecliptic (sun's path) and celestial equator intersect. There's no particularly bright star at this "0" point, however, the two stars along the eastern side of the Great Square of Pegasus make good substitutes. They're close enough to 0h R.A. that you can picture them as defining 0 hours of R.A. From there east, R.A. increases.
The best reference for R.A. calculations is a sidereal clock! Luckily, they come cheap on the Internet. Here's one at the link: http://www.jgiesen.de/astro/astroJS/siderealClock/ Put in your longitude, and you're good to go! Remember that the time on the clock the R.A. that is crossing YOUR LOCAL meridian at the time shown or selected.
You must be logged in to post a comment.
LuigiLikesAstronomy
June 4, 2023 at 11:15 am
I want to thank the author a lot of this life saving article! I was writing something for school and I couldn't find anything simple and well written enough about the topic, with most of the results being college texts. To my surprise, there were even all these beautiful diagrams that made everything even clearer. Thank you so much for taking the time to write this!
You must be logged in to post a comment.
Bob KingPost Author
June 4, 2023 at 11:44 am
Dear Luigi,
Thank you for writing. I'm so happy you found the article useful!
You must be logged in to post a comment.
You must be logged in to post a comment.