We journey to distant suns to look back at our solar system and see its place among the stars.

Bob King
Something like 9,100 stars are visible with the naked eye across the entire planet. Each appears in a particular constellation and shines with a specific magnitude, unless it's a variable star like Algol, in which case its brightness varies. From each one of these stars we might imagine looking back towards the Sun, which shines in each of their skies as surely as they do in ours.
Depending on that star's distance from us the Sun may appear bright or faint. From the neighboring star system Alpha Centauri, 4.4 light-years distant, it shines at magnitude +0.5, nearly as bright as Procyon in Canis Minor. But from far-flung Deneb at about 2,600 light-years you'd need dark skies and an 8-inch telescope to spot the 14.3-magnitude speck.
Winter can be confining. Maybe that's what inspired my desire to figuratively leave the solar system and see it from other points of view. This got me wondering how bright the Sun would be and in what constellation it would appear when viewed from a planet — imaginary or real — orbiting one or more of the familiar bright stars?
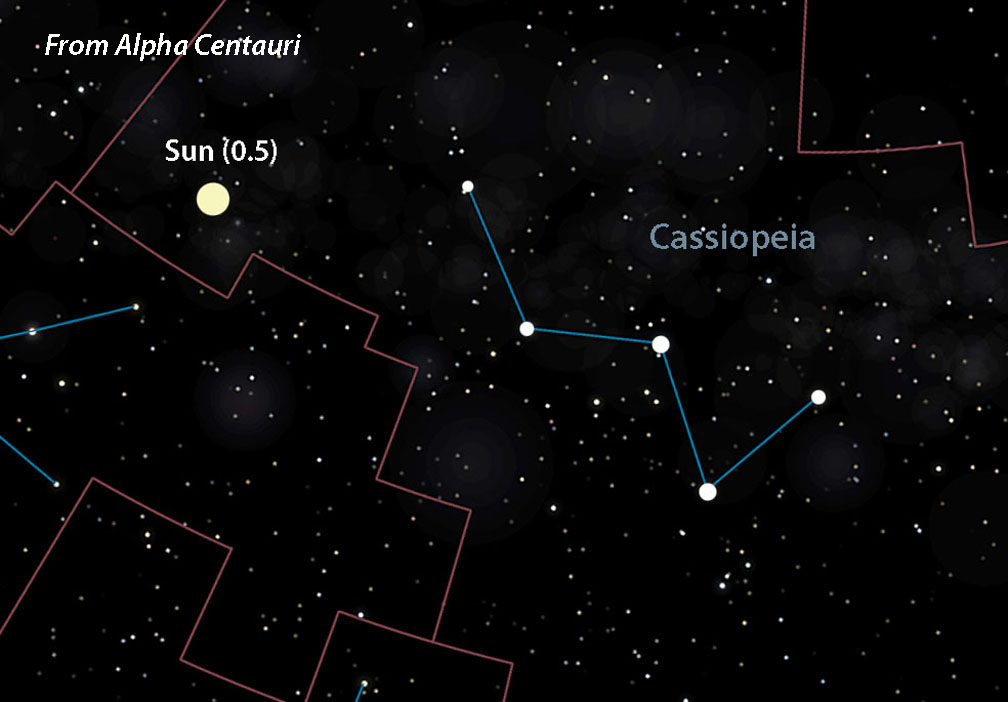
Celestia (with additions by Bob King)
Magnitude mastery
First, we'll need to calculate the Sun's apparent magnitude from a specific distance. For that you'll use the formula for determining a star's absolute magnitude but solve for apparent magnitude instead. Here's one iteration of this gem of mathematical magic:
m-M = 5 log(d/10)
We'll have to plug in M = absolute magnitude of the Sun and d = distance to a star of our choosing in parsecs. Once we know these values, we can do the math to find m, the Sun's apparent magnitude at the distance of that selected star.
The Sun's absolute magnitude, M, or how bright it would appear at a standard distance of 10 parsecs (32.6 light-years), is the easy one to plug in since we already know it. Absolute magnitudes provide a standard reference for directly comparing stars' true luminosities. The Sun has an absolute magnitude of 4.8, a considerable step down from its apparent brightness of 26.7!
NRAO / AUI / NSF
Please pass the parsecs
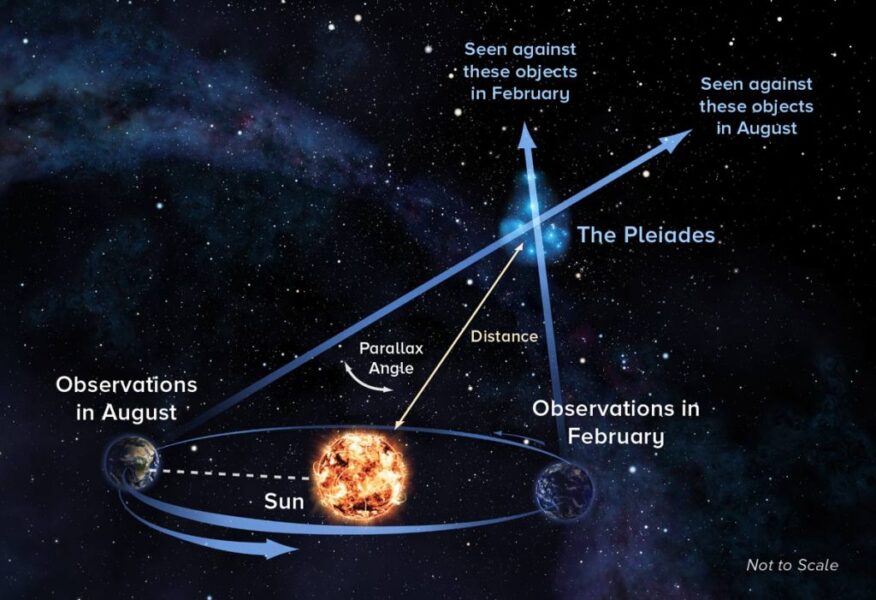
It's easy to look up a star's distance (d), but depending on your source, you might find it quoted in light-years — and so you'll have to convert to parsecs. A parsec is equal to 3.26 light-years, which is the distance at which the radius of Earth's orbit subtends an angle of one arc-second. A star located one parsec away would have a parallax of one arcsecond. Proxima Centauri, the closest star to the Sun, has the greatest parallax, equal to 0.77 arcsecond.
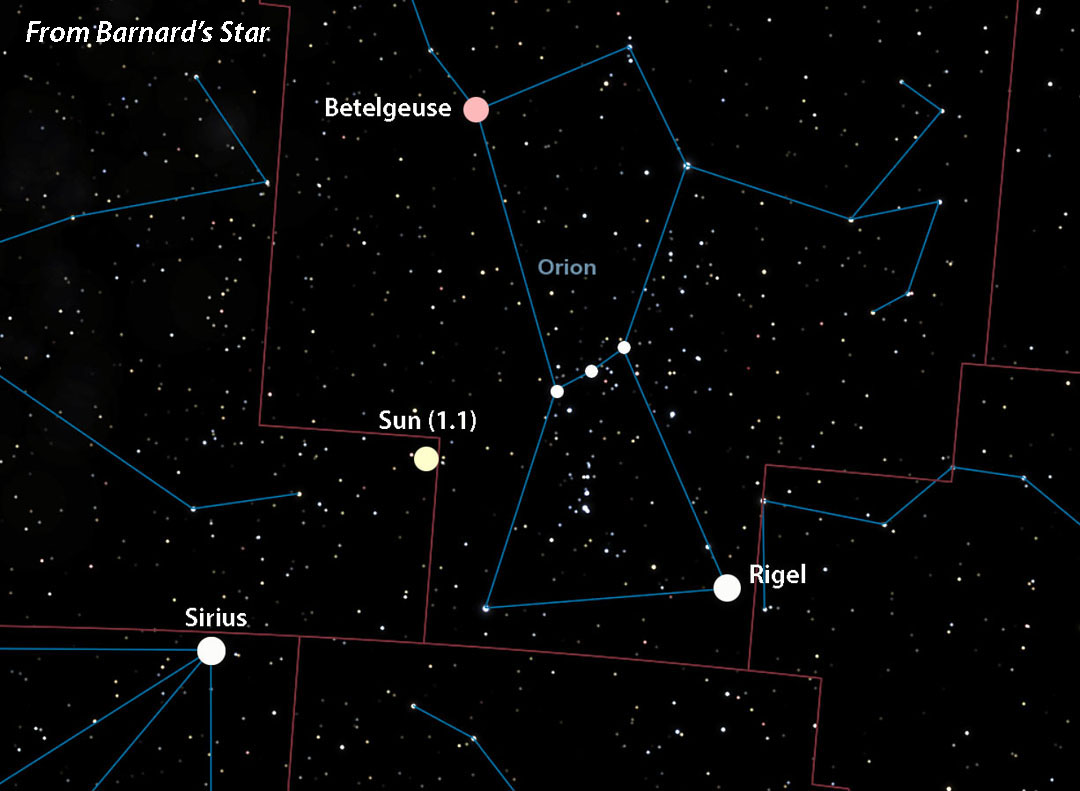
Celestia (with additions by Bob King)
Many online converters will help you make parsecs out of light-years. I found this one straightforward, mostly ad-free, and with a host of fascinating options, including a conversion from light-years to cubits! (If you've never heard of a cubit, it's an ancient unit of measure equaling the length of the forearm from the elbow to the tip of the middle finger . . . it's derived from the Latin for "elbow," in fact.)
Good one-stop shops for stellar distances include the Abrams Planetarium list of the 100 brightest stars or any recent volume of the Royal Astronomical Society of Canada's Observer's Handbook.
Now you have everything you need to solve for the Sun's apparent brightness from your star of choice. Copy and paste the equation into an equation solver (OK, I'm lazy), put in the values for M and d (remember, it's parsecs only), and out comes m. So much fun. I use MathPapa, but there are many others.
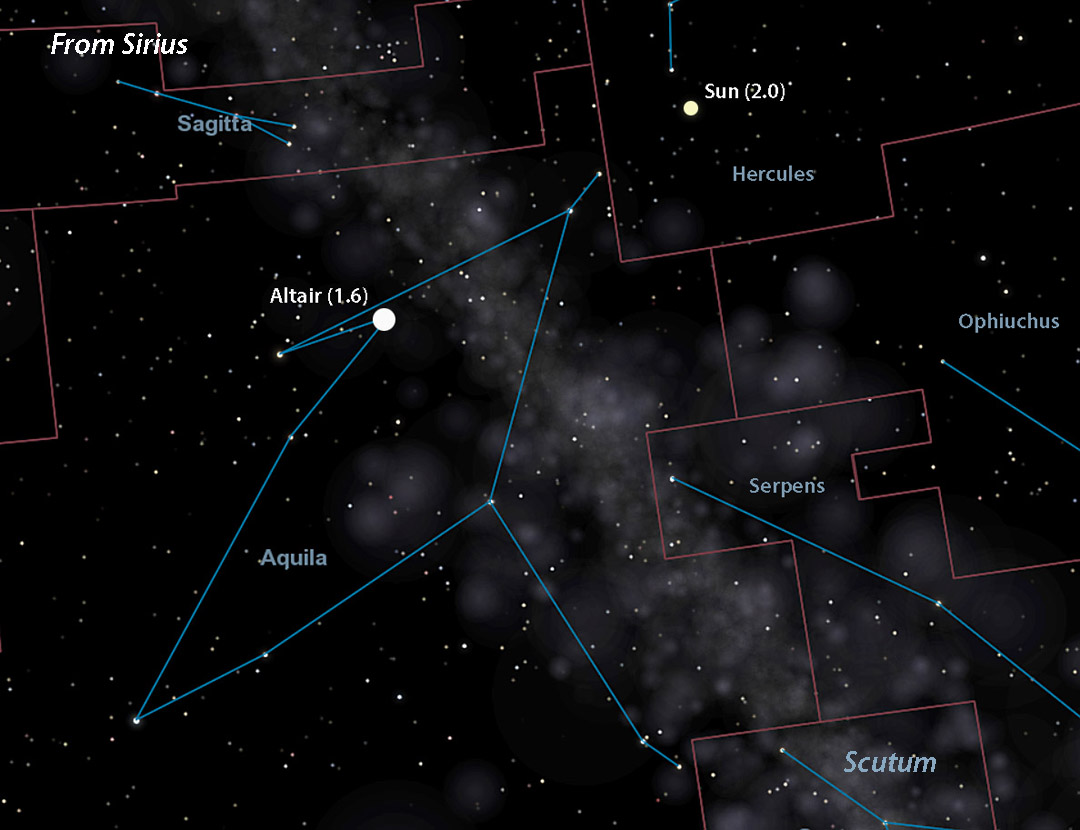
Celestia (with additions by Bob King)
Sunshine at Arcturus
Here are some examples of the Sun's apparent magnitude as seen from some familiar stars:
- Alpha Centauri = +0.5
- Sirius = 1.9
- Procyon = 2.5
- Altair = 3.4
- Vega = 4.2
- Pollux = 4.9
- Arcturus = 5.1
- Capella = 5.4
- Aldebaran = 6.3
- Regulus = 6.7
- Spica = 9.3
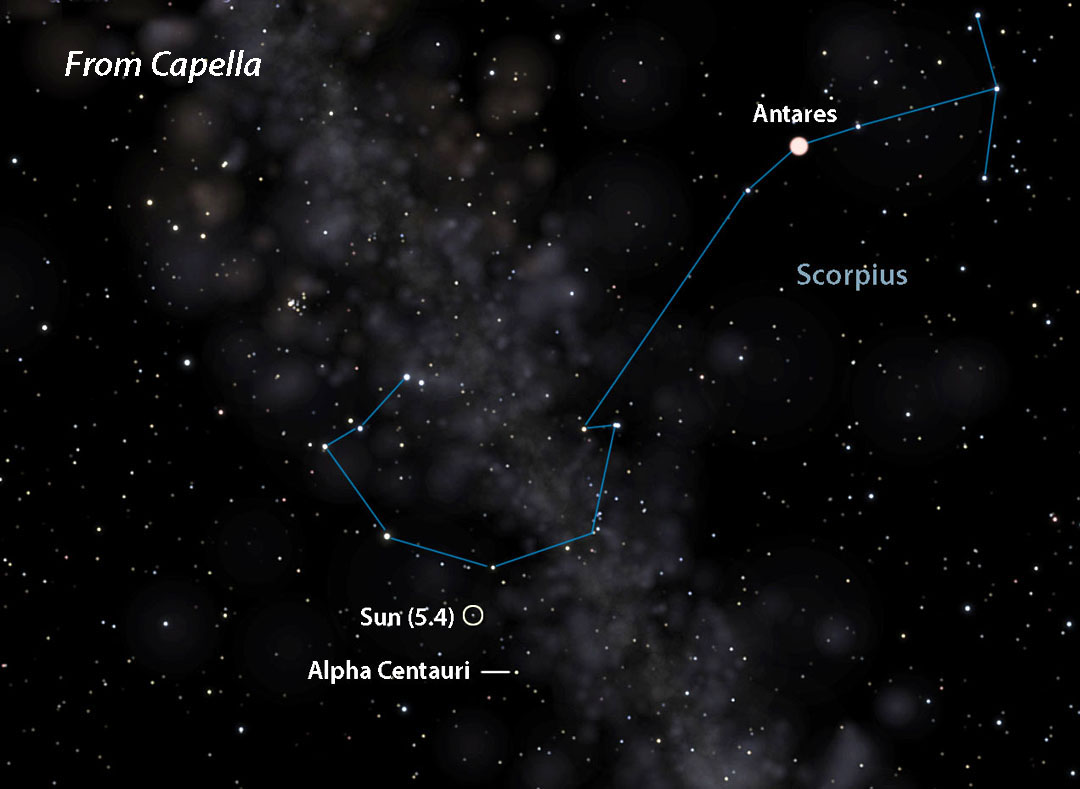
- Antares = 11.0
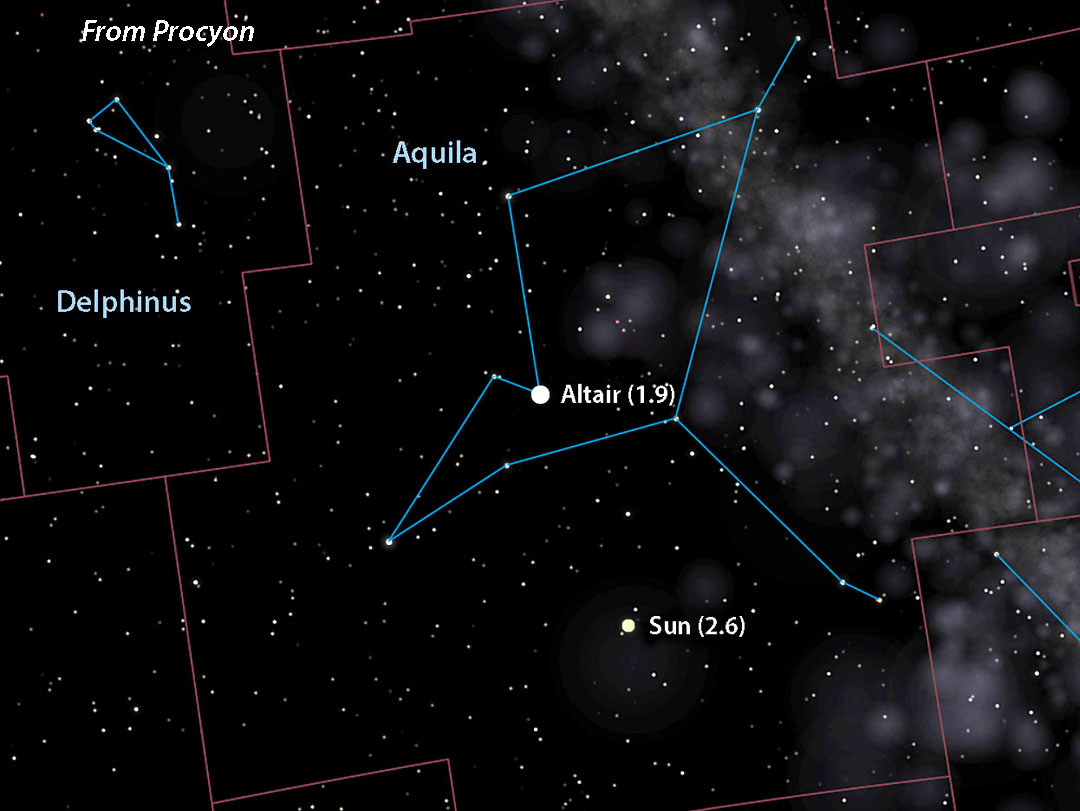
Celestia (with additions by Bob King)
Once we know the Sun's apparent brightness, we'll next want to recreate its appearance from an alien star system's sky. For that we'll need two things: its celestial coordinates as seen from the star and the positions of familiar stars and constellations from the point of view of an observer at that location.
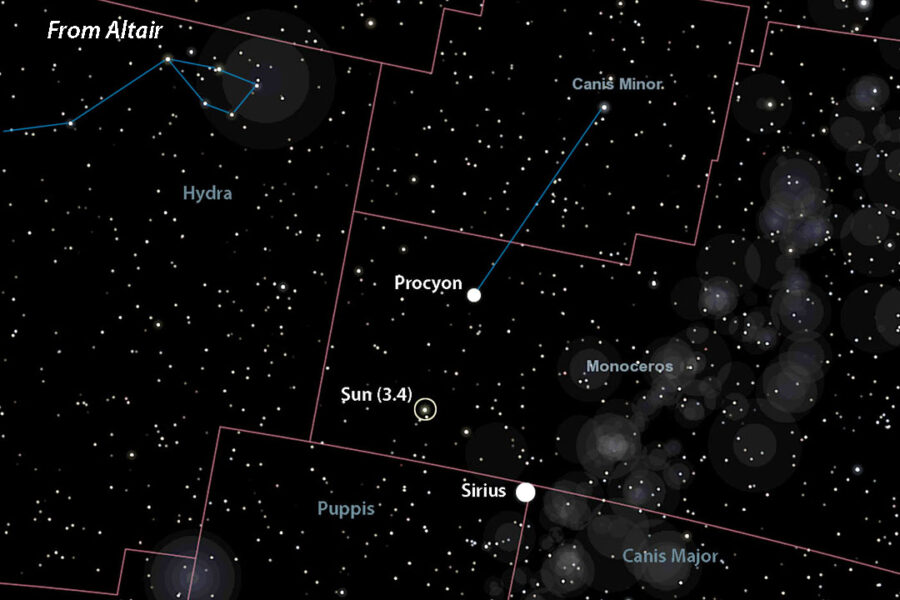
Celestia (with additions by Bob King)
Let's choose Sirius, located at R.A. 6h 45m, Dec. –16° 43′. To find the point in the sky directly opposite Sirius — where you'd see the Sun from that star — just add 12 hours of R.A. and reverse the declination sign. That puts the Sun (now 2nd magnitude) at R.A. 18h 45m, Dec. +16° 43′ in southeastern Hercules. If adding 12 hours to the R.A. shoots it past 24 hours, subtract 24 from that number for the correct right ascension.
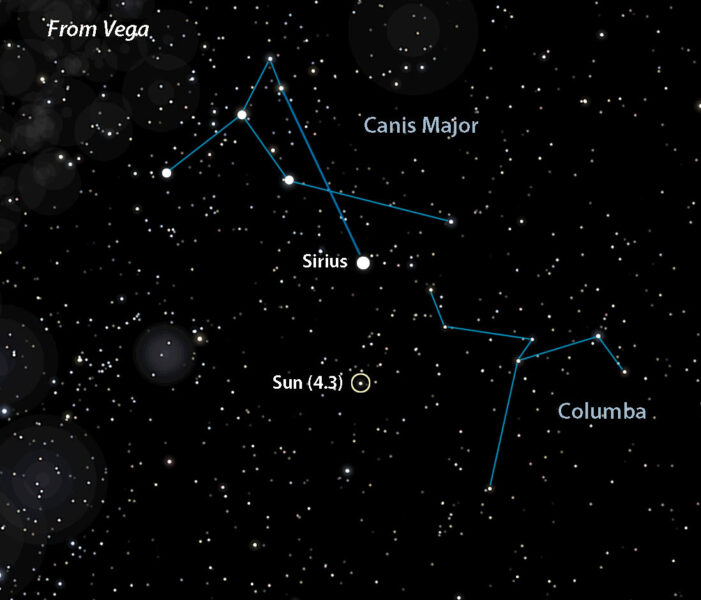
Celestia (with additions by Bob King)
A crushed teapot?
Although stars appear pasted on a flat sky, space is obviously three-dimensional — 4D really, but three will do for our purposes. When you jump from one star to another, its neighbors also shift around. This can seriously alter a constellation's outline compared to the view from Earth. The farther you travel, the more bent out of shape the constellations become. To prevent warp-overload I chose only relatively close stars. Once you get beyond 50 light-years or so, depending on the region of the sky, star patterns and their magnitudes quickly become unfamiliar. In fact, I was amazed at how malleable the patterns were given the relatively modest distances I "traveled."
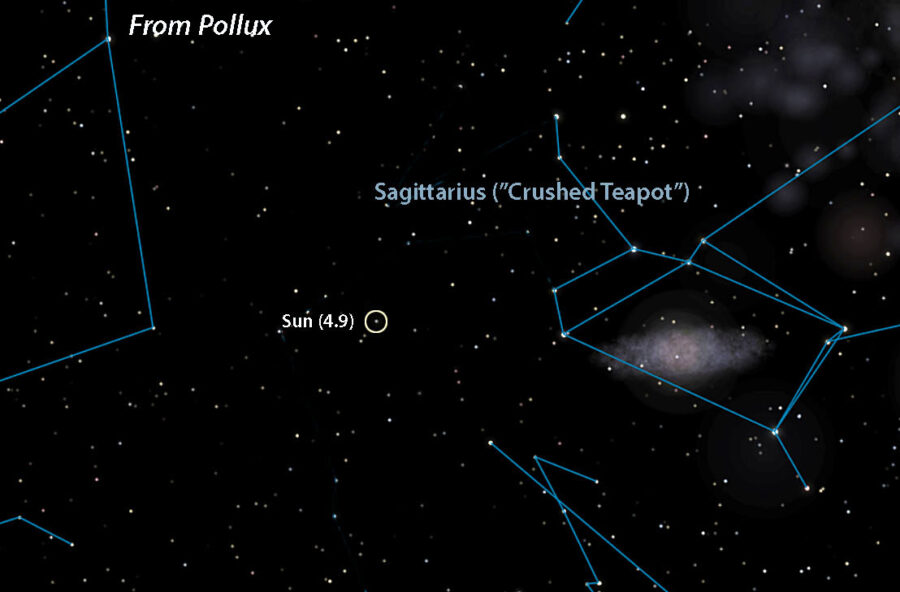
Celestia (with additions by Bob King)
For my mode of transportation I chose the free space simulator Celestia, which is available for Windows, Linux, macOS, iOS and Android. I had to play around with it a bit and add a few of my own enhancements, but it does a great job plotting the Sun's location from when you're far at home. Be aware that its range of "dot" sizes to depict stars is limited, so I tried my best to represent the Sun and other key stars as you'd see them visually. Please take these representations with a grain of interstellar dust.
Celestia (with additions by Bob King)
The jaunts were not only fun and instructive, but if there was any Sun-centered, lingering Copernicanism left in my veins when I began this journey, I arrived home more unmoored than ever. Not that that's a bad thing. Picturing the Sun's place in the firmaments of its fellow suns opened up my mind to what it means to be a star among many.
 16
16









Comments
albert poncedeleon
February 2, 2022 at 3:31 pm
Thanks Mr. King. Bob King, does it again!! A great article. I always had the same curiosity; how do we look from other sites of the universe? A very illustrated and graphic views and surprising how big or small our sun may be seen depending on the angle and location of the viewpoint. Great article, thanks again.
You must be logged in to post a comment.
Bob KingPost Author
February 2, 2022 at 4:11 pm
Dear Albert,
That is so kind of you — thank you! Happy (stellar) trails!
You must be logged in to post a comment.
bob kelly
February 2, 2022 at 5:05 pm
Wonderful work to show us these alternative views!
Since Vega's pole points toward our Sun, I often told stories at star parties that any planets orbiting Vega might have our Sun as a pole star. But, as we found out at a star party (and shown by your diagram), any Vegan folks would be more likely to use further away but much brighter Sirius as a marker for their pole in the sky.
Of course, that's if any planets have the same inclination as their sun. As we know, Earth is 23 degrees different from our Sun's pole.
We found this when a young kid, playing with the parents' phone with Vega overhead, pointed the phone at the ground and saw Sirius through the ground on the other side of the world from Vega.
You must be logged in to post a comment.
Bob KingPost Author
February 2, 2022 at 11:21 pm
Hi Bob,
Thank you! Glad you enjoyed them. Yes, that's right about Vega. I remember reading that we see the star pole-on, so yes, our sun would be the pole star from any putative planets with low axial inclination there. And though old Sol would be on the faint side, it would still be a mag. brighter than our own southern pole star, Sigma Octantis.
You must be logged in to post a comment.
Shawn Quinn
February 3, 2022 at 6:52 am
Wow, this article was fantastic! I often wondered the same while stargazing going back to my childhood. Well done and thanks Bob!
You must be logged in to post a comment.
Bob KingPost Author
February 3, 2022 at 2:24 pm
Dear Shawn,
Thank you! I'm tickled. Glad you enjoyed these perspectives.
You must be logged in to post a comment.
Tom-Traub
February 4, 2022 at 6:58 pm
Great article. I was a senior in high school when the March 1975 article on The Sky from Capella captured my interest on space travel and our place in the universe. I wrote a program based on that article to look at the sky from various stars using the School Districts mainframe. No one else understood what was being produced until I explained it and then they were amazed. I enjoyed going back to that same amazement after reading the article. Maybe this will spur on others like it did to me.
You must be logged in to post a comment.
Bob KingPost Author
February 5, 2022 at 12:20 am
Hi Tom,
You were way ahead of your time. I hope you were able to share the views with your fellow students back then. Glad you enjoyed the article — thank you for writing!
You must be logged in to post a comment.
ErnieOstuno
February 6, 2022 at 1:14 am
This is a great sampling of perspective in our stellar neighborhood. I was trying to figure out why Sirius moved so much compared to the triangle asterism formed by Adhara, Aludra and Wezen as seen from Vega and Earth, then realized that those three stars are hundreds of light years distant while Sirius is much closer to the sun and Vega. Similar to seeing nearby stationary objects moving greater apparent distances than distant objects while traveling down a highway.
You must be logged in to post a comment.
Bob KingPost Author
February 7, 2022 at 5:40 pm
Hi Ernie,
Exactly! Closer stars move greater apparent distances compared to stars in the remote background.
You must be logged in to post a comment.
AB
February 8, 2022 at 7:09 pm
That was really cool. I'm only a casual, though appreciative, observer, so the math is more than I would pursue, so, thanks for doing it for us the readers 🙂
Perhaps in the future you can show us some more "alien skies" from a new set of stars.
You must be logged in to post a comment.
Tom Hoffelder
February 16, 2022 at 8:23 pm
Hello Bob, I agree with all those above, an excellent article with the last image being the most interesting. Only 43 ly away and the sun drops to less than 5th mag, with Alpha Cen nearby (and brighter?) in the sky.
However, the image used to explain parallax is the right idea but, as you noted, the parallax of the nearest star is less than one arcsecond, which means the parallax of the Pleiades is much smaller. And yet, the diagram indicates the Plieades move (as near as I can tell) from approximately Cetus to Perseus in six months. I know you, and everyone here, know the Pleiades, or any star, stay where they belong, to the unaided eye and even in our scopes, regardless of where the Earth is in its orbit. That is probably why no one else bothered to say anything but I couldn't help myself, so please accept my apologies.
On the bright side, in trying to find an example of real parallax, I discovered this NASA article from June 2020. It shows the parallax of Proxima Centauri and Wolf 359 (~8 ly distant) based on more than a 4 billion mile baseline, the distance between Earth and the New Horizons spacecraft at the time. So another good thing resulting from your article! https://www.nasa.gov/feature/nasa-s-new-horizons-conducts-the-first-interstellar-parallax-experiment
You must be logged in to post a comment.
Kye
February 17, 2022 at 7:53 pm
Thanks for the link, Tom! Such amazing stuff in the nasa site, it's a shame it doesn't get noticed more easily!!!
You must be logged in to post a comment.
Kye
February 17, 2022 at 7:58 pm
Hey Bob! Catching up with this article thanks to Tom H's heads-up. Very interesting, and great stuff to be able to tell newbies when we get them out looking at the stars. I have been using Celestia for the last couple years as I (and a friend) work our way through writing a space adventure novel about some amateur astronomers finding themselves on a planet orbiting Epsilon Indi, a VERY interesting little system, about 12 lightyears away. We worked up some "what the constellations would look like" details so that we could make the exo-star party they have there as realistic as possible. From that distance, there are quite a few similarities to our sky, yet some very interesting differences...
You must be logged in to post a comment.
Bob KingPost Author
February 18, 2022 at 2:09 pm
Hi Kye,
Thank you, and I love the idea of an exo-star party. Brilliant!
You must be logged in to post a comment.
Dileep
November 25, 2023 at 8:55 pm
Hi Bob
Thank you for the article. Where can I get the image "the view from Vega", in this article, to use in a book?
Thank you
Dileep
You must be logged in to post a comment.
You must be logged in to post a comment.