Want to see a star rock in real time? Observe the Sun in the crimson light of hydrogen alpha (h-alpha), and watch it come alive.

Bob King
A chill autumn morning, but the Sun is out. I feel its heat on my cheek and in my mind follow the radiation back to its source 93 million miles away, a star so bright it hurts my eyes to look at it. The Sun radiates abundant light, so much so that to view it safely we must use filters that allow only a fraction of a percent of that light into our eyes.
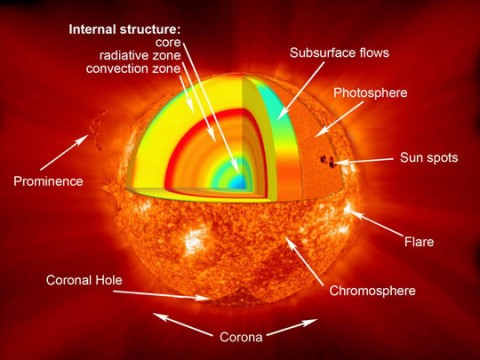
So protected, we can study the nearest star in either white light or choose among several narrow wavelengths, the most common of which are red hydrogen-alpha and violet calcium K-line light. White light filters reveal the glaring face of the Sun called the photosphere, home to granulation, a rice-grain texture of rising and sinking convective cells; faculae, bright patches of concentrated magnetic energy; and sunspot groups that come and go as the rotating Sun carries them in and out of view.
NASA
White light filters provide a simple and inexpensive way to get to know the Sun; they allow us to see day-to-day and week-to-week changes in photospheric activity. But if it's real-time excitement you're looking for, nothing matches the view through an H-alpha (Hα) filter. Viewed in a narrow slice of the spectrum centered in the ruby-red H-alpha line, the Sun throbs with activity.
Prominences, spicules, fibrils, Ellerman bombs, flares and more seethe and boil before your eyes. Unlike the more sedate white light view, H-alpha pulls back the curtain to expose the beast for what it is: a ferocious, unpredictable ball of incandescent hydrogen gas. I'll never forget my first view of a flare through a 0.7Å (angstrom) Daystar H-alpha filter. Ribbons of gas grew to a fiery brightness — brighter than anything else on the Sun — right before my eyes. I watched with a mix of awe and fear. Ever since that time, I've seen the Sun not so much as a sunny companion but as a star to be reckoned with.

©Alan Friedman/avertedimagination.com
H-alpha light is emitted by hydrogen atoms, by far the most common element in the Sun, when electrons within those atoms absorb energy and rise to a higher energy level or orbit. When they cascade back to their original orbits, they release that energy as crimson light with a wavelength of 6562.8Å (656 nm).

Alson Wong
The process occurs with great efficiency in the 1,250-mile-thick layer of solar atmosphere located just above the photosphere called the chromosphere. Here, the temperature rises from about 11,000°F to 36,000°F, hot enough to excite hydrogen to emit its singular red light. "Chromo" means color and refers to the picturesque red flames or prominences seen around the limb of the Sun when its overly-brilliant photosphere is covered up by the Moon in a total solar eclipse. The prominences, like other features visible in H-alpha light, are always there but completely swamped by photospheric glare. You either have to chase down a total eclipse to view them, or more conveniently, get a hold of a hydrogen alpha filter.
By selectively "slicing and dicing" all the other colors from sunlight until you're left with only a razor-thin slice of red light, H-alpha filters essentially create an artificial eclipse any sunny day of the year. They're even better than eclipses in one respect — not only are prominences visible, but so too are a host of other phenomena hidden for ages from human sight.

Bob King
H-alpha filters work by rejecting all but the narrow sliver of H-alpha light. They accomplish this feat in several steps: a red glass pre-filter over the telescope objective removes most of the shorter, bluer wavelengths at the outset, letting only red light pass through to a Fabry-Perot etalon and dichroic or blocking filter at the eyepiece end of the scope. These filters work in concert by removing unwanted light through destructive interference — the canceling out of specific wavelengths through multiple reflections — and constructive interference, where the desired wavelength is amplified and sent along to the eye.
The etalon weeds out unwanted light this way and sends the remainder to the blocking filter which removes the rest and transmits only the desired H-alpha slice.
In some of the small, dedicated H-alpha scopes available, the etalon, pre-filter, and blocking filters may be in different arrangement, but no matter the scope, they all single out the H-alpha line through a combination of filtering and destructive/constructive interference. In addition to temperature-controlled heaters for Doppler studies, smaller scopes use a mechanical tilting mechanism or "pressure tuning" to vary the wavelength of red light in small increments for Doppler studies.

Bob King
The narrower the filter wavelength, the more off-band light is eliminated and the greater the contrast, all crucial factors for seeing details in the chromosphere. A filter with a passband of 0.7Å to 0.5Å will show both excellent surface detail and prominences, while one that transmits in the 0.9Å to 2Å range will still offer fine views of prominences, but disk details will be hard to make out due to lower contrast, i.e., too much light.

Alvaro Ibanez Perez (left) and Greg Piepol / Sungazer.net (right)
Filters and small, dedicated H-alpha refracting telescopes range in price from around $700 for a Coronado PST (Personal Solar Telescope) to $14,000 for a 0.3Å Daystar standard edition Quantum SE filter. Several companies make H-alpha filters and telescopes for amateurs:
- Lunt Solar Systems: Filter packages and dedicated solar telescopes
- Coronado (sold through Meade and other outlets): Filter packages and dedicated solar telescopes
- Daystar filters: Filter packages and the Quark H-alpha "eyepiece"
- Baader Planetarium: Filter packages
Back in the 1980s, only filters were available, and you had to buy a smaller pre-filter to attenuate the Sun's light and increase the telescope's focal ratio to f/30 to provide the parallel light rays the filter required to work properly. Since the introduction of the Coronado PST, the market has expanded into small, dedicated scope–filter combos that make doing H-alpha quick, easy, and more portable. Less expensive, too. You can pick up a typical unit for around $1,000 or less. A recent check on the Cloudy Nights classified advertising site turned up several small, used H-alpha scopes for around $450. With the H-alpha renaissance still going strong, there's no better time to make that step into H-a.
Greg Piepol / Sungazer.net
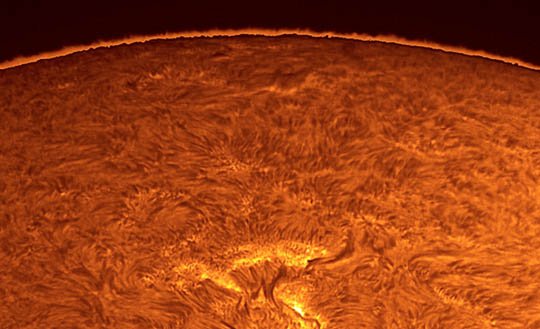
Once you have your filter or dedicated telescope set up and pointed at the Sun, what should you expect to see? Lots! I was first taken by the spicules (SPICK-yools) which run all the way around the edge of the solar disk and look exactly like red fur. Reality check. They're jets of hot gas between 2,000 to 6,000 miles (3,000-10,000 km) high, seen in profile. If conditions allow, try magnifying a small group of them to 100x or higher and see how long they maintain their shapes. Most last only 15 minutes before morphing into new spicules. Ever abundant, nature has seen to it that some 300,000 active spicules roil the chromosphere at any given moment.

Bob Antol / stargate4173.com
Much larger than spicules and one of H-alpha's greatest highlights are the prominences. Appearing along the solar circumference, even small ones routinely dwarf Earth. Prominences are broadly divided into two categories: quiescent and active. Quiescent prominences look like hedgerows or bushes with much internal branching structure. If you keep a close watch, even one of these "quiet proms" will show structural changes in as few as 10 minutes. They're also prone to flinging part of themselves higher up in the corona in a slow-motion sort of way before the material recollects and settles back down into the chromosphere. A lava lamp comes to mind.
Active prominences are associated with flares and can be seen at the limb as brilliant blobs or, more rarely, as nested loops or sprays. If you spot one, DO NOT turn away. Surging and shape-changing in real time, not only will they take your breath away but potentially make you late for work. Ahem.

Greg Piepol / Sungazer.net
Prominences can last for many days, which means they get carried across the face of the Sun as it rotates. Seen against the bright solar disk, they're called filaments and look like bushy eyebrows and sinuous snakes with small, dark anchor points that remind me of caterpillar "feet". If you're lucky, a bright prominence will extend well into the disk as a dark filament, and you'll get to see how they're one and the same. The unique placement also reveals the prominence/filament as a grand three-dimensional arch, a sight guaranteed to ping your awe meter. Filaments can stretch halfway or more across the Sun.
Moving further into the disk, you'll suddenly realize where all that 1970s shag carpeting disappeared to. It's all over the chromosphere! What you're seeing is combination of spicules — which appear dark against the disk — and bundles of fibrils, hot plasma confined in magnetic tubes, that give the Sun a dark, mottled and swirly appearance.
Running like tendrils of glitter between and the dark mottles are tiny, moderately bright points of light called filigree. Filigree define the chromospheric network, a web-like network that outlines the Sun's supergranules, giant convective cells that transfer energy from deep beneath the photosphere up to the surface. Filigree concentrate along their edges.

Alvaro Ibañez Perez / flickr.com/photos/kokehtz/
Much more obvious when looking at the H-alpha Sun for the first time are the bright, patchy plages (PLAH-jez) that mark the sites of active regions or sunspot groups. Don't be surprised if you see plage where no spot group is visible in white light. These are emerging flux regions (ERFs) where a magnetic flux tube is just breaching the surface on its way to producing a bipolar sunspot group.
As for sunspots, their dark cores or umbrae look similar to what you see in white light, but the penumbrae branch out into impressive whirls of fibrils and spicules. When the seeing is excellent, you'll see an overwhelming amount of fibril/filament and plage detail in large sunspot groups. I used to attempt to draw them but with only one life to live, soon settled on sketching just the basic outlines.

Greg Piepol / Sungazer.net
It's sometimes easy to confuse bright plage with a weak flare. Close inspection of large, complex plages often reveals tiny, brighter kernels of light that fluctuate in brightness. These are likely Ellerman bombs (named for an early 20th century astronomer who studied them) or tiny microflares that come and go within 5 minutes. Flares are unmistakable and involve a sudden brightening within a sunspot group often as multiple ribbons that resemble flows of white-hot lava. They can last from a few minutes to hours and change in both intensity and area in real time right before your eyes. Raw star power.
Every one of these and much more will reveal themselves to the H-alpha observer over time. During a typical viewing session, I often look at the Sun first in white light to inform my observations in the deep red. Once the filter is warmed up and ready to go, I leave it on for a couple hours for the sheer pleasure of returning time and again to see what's changed or to (hopefully) catch a flare in action. In between I'll read, eat, or invite the neighbors over for a look.
When you read of a large, rapidly developing sunspot group with a complex "delta" magnetic field, get the H-alpha scope at the next opportunity to improve your chances of seeing active prominences and the ultimate prize, a large flare.
Helpful Resources to Learn More About H-alpha Sun:
- Prairie Astronomy Club H-alpha observing guide
- Cloudy Nights Solar Observing and Imaging Forum (Great place to see current H-alpha images, get questions answered by expert amateurs)
- NOAA Solar Region Summary (Sign up for the Solar Region Summary and other Sun-related subscription services sent directly to your e-mail)
- Big Bear Solar Observatory (The link I selected will take you to the latest full-disk images of the Sun in H-alpha)
- Solar Dynamics Observatory latest images
- A.L.P.O Solar Section
- Astronomical League Hydrogen-Alpha Solar Observing Program
- The Sungrazer Observatory (Fine amateur photographs by imager Greg Piepol)
- Solar Flare Classification
 12
12








Comments
Peter Wilson
September 24, 2015 at 11:02 am
"When they cascade back to their original orbits, they release that energy as crimson light with a wavelength of 6562.8Å (656 nm)."
True enough, but the reverse also happens, and a photograph of the Sun's spectrum shows a dark-band at the H-alpha wavelength, not a bright line. The absorption process completely overwhelms emission.
It seems like it is the narrowness of the filter that produces the details, not the particular wavelength. Is there some more subtle reason for observing at a wavelength that is mostly absent?
You must be logged in to post a comment.
Stephen-Ramsden
September 24, 2015 at 7:31 pm
Peter, The absorption lines of H-Alpha and CaK are produced by H and Ca atoms in the chromosphere absorbing portions of the continuous spectrum emitted by the Sun's photosphere.
The re-emission lines of both events are against the backdrop of the absorption line thus framing them perfectly with a totally black background for filters with small enough bandpasses.
This phenomena offers the re-emission lines with very little darkening required by the telescope as opposed to a white light wedge which would darken photospheric light to 1/10,000th its original magnitude and losing a commensurate amount of resolution and detail.
You must be logged in to post a comment.
gd62390
February 7, 2017 at 12:11 pm
Hello!
My name is Roger and I'm buying a Coronado SolarMax II 60 double stack with BF-15, partly due to the info in this article. This will be my first solar telescope and I plan on recording the solar eclipse in August and I was wondering if totality will be bright enough to be recorded through the scope. I'm guessing not since you can look directly at the sun during totality. Just trying to plan ahead and figure it all out. Thanks for any input.
You must be logged in to post a comment.
Bob KingPost Author
February 7, 2017 at 1:50 pm
Hi Roger,
Yes, you'll be able to record the prominences surrounding the black disk of the moon but not the corona. For that, go filterless.
You must be logged in to post a comment.
bluecat_013
April 3, 2017 at 3:31 pm
I'm considering getting a solar scope; I have about $1500 and both my son and I love solar viewing. He'd like to try some solar imaging. What is the difference between the 5mm, 10mm and 15mm blocking filter that also seems to increase the price of the telescope? I would assume the 15mm is the preferable one, but what exactly does it do, and what is the difference in the image, if any? And of course, is there a "better" solar scope out there; one you would recommend, at least in our price range? Lunt over Coronado? etc. etc. etc.
You must be logged in to post a comment.
Bob KingPost Author
April 3, 2017 at 3:58 pm
Hi bluecat,
Glad to hear you guys are into solar observing. Blocking filters are a key component -- they help narrow the sun's white light to pure H-alpha. It's not so much that one blocking filter is better than another. Each is specific to your telescope's focal length: you get the right one to fit the focal length. I wish I could make a recommendation regarding Lunt vs. Coronado, but I've had little experience with those except for the Coronado PST which I thought was OK but not nearly as nice as my personal 0.7 A Daystar. I would suggest you check out the Solar Observing Forum on cloudynights.com Here is some additional info on blocking filters and focal lengths to help your decide: http://bit.ly/2oCjhZQ
You must be logged in to post a comment.
Hodgepodge
April 19, 2017 at 7:24 am
Hi Bob.
I am relatively new to astronomy (and have a newbie kind of question) I have recently got the itch to view the sun and all it's beautiful features. I would love to see the details that a hydrogen alpha filter provides. I have a question that seems extremely simple but I haven't seen anything anywhere on if it would work. I see that the PST scopes have the hydrogen filter at the front of the aperture. I have an 8 inch dobsonian, and it has a dust cap with a 2" removable hole. I also have a 2" to 1.25 eyepiece converter. So, if I simply put the hydrogen filter over the dust cap hole, would it work? I have read that a standard white light filter plus the hydrogen filter in the eyepiece would just give you a deep red version of the normal solar filter view, but what about this idea.
You must be logged in to post a comment.
Bob KingPost Author
April 19, 2017 at 8:38 am
Dear H.,
I wish it were so, but if I understand you correctly, this idea wouldn't work. An H-alpha filter has two parts: a red pre-filter that's placed in front of the telescope's objective and a special filter assembly at the back/eyepiece end that blocks all the remaining light except the specific wavelength of H-alpha.
You must be logged in to post a comment.
Hodgepodge
April 20, 2017 at 5:47 am
Ah. I guess if it worked everyone would be doing it. Okay. I'll still get a polymer/mylar filter though. Maybe one day I'll get one of the affordable PSTs. Thanks!
You must be logged in to post a comment.
Bob KingPost Author
April 20, 2017 at 9:48 am
Hodgepodge,
Keep an eye out for a used H-alpha setup on cloudynights.com That can be a great way to go.
You must be logged in to post a comment.
SamOfSiam
September 5, 2017 at 8:54 pm
Hi Bob, thanks for the article. I am curious on the differences between the 40mm, 60mm, and 90mm? I know for dark skies, bigger aperture equals more light gathering, but in this case, you are observing the sun, so why need a larger aperature? Thanks in advance.
You must be logged in to post a comment.
Bob KingPost Author
September 5, 2017 at 10:36 pm
Hi Sam,
Thanks for asking. Based on my experience with larger and smaller apertures, the larger aperture shows finer details and also gives a brighter image at higher magnifications. But at low power, they appear similar.
You must be logged in to post a comment.
You must be logged in to post a comment.