For the most part, scientists have come to terms with the existence of an unknown antigravity force permeating the cosmos. This "dark energy" — a conveniently ambiguous term for something no one understands — sticks its nose into cosmology on a regular basis and, increasingly, won't be denied.
While we're nowhere near cracking dark energy's secrets, a team of astronomers from the University of Hawaii's Institute for Astronomy has confirmed its effects on the microwave background radiation we see from the early universe. The team's data also confirm theories that large-scale cosmic structures — shaped in part by dark energy — should give rise to anomalies in this radiation.
The astronomers, led by István Szapudi, looked for what's called the late-time integrated Sachs-Wolfe (ISW) effect. It's a lot of words to describe something relatively straightforward:

The masses of a galaxy supercluster makes a relatively deep well in space-time, represented here in two dimensions. The more massive an object, the deeper the well — if the mass is not spread out too far.
Casey Reed
Imagine a rubber sheet stretched taut. If you take, say, five dinner plates and set them close to each other on the sheet, they create a deep valley. If instead you spread the plates farther out on the sheet, they'll make a shallower valley.
Now add the astronomy: the plates are the galaxies of a gigantic supercluster 500 million light-years across. The sheet is space-time, and the galaxies in it move apart from each other because space-time is expanding like stretched rubber. (That's what astronomers mean by "expansion of the universe.") Dark energy speeds up the rate of this expansion.
A photon from the far background travels toward you though space-time like a marble rolling on the sheet. It falls down one side of the supercluster's valley, thereby gaining a little energy. In a non-expanding universe, the photon would use up that same amount of energy when it climbed the opposite side, with no net effect.
But in an expanding universe, space-time stretches and the supercluster's valley flattens out during the photon's 500-million-year journey across the valley. When the photo arrives at the other side, the hill it climbs up is shorter than the hill it first went down. So the photon keeps some of the energy that it gained when falling in. This difference appears as a temperature increase — in this case, a change of ninety millionths of one kelvin (i.e. really really small).
On the other hand, if the photon first climbed up a hill — a region with a below-average number of galaxies such as a supervoid — that hill would be lower by the time the photon came back down. The photon would never regain all the energy it lost by climbing. In this case, the photon would be slightly colder.
That's the late-time integrated Sachs-Wolfe effect.

In this all-sky map, NASA's Wilkinson Microwave Anisotropy Probe (WMAP) records minuscule temperature fluctuations in the CMB as different colors. These fluctuations are the noise that Szapudi's team had to overcome.
The Hawaii team studied this effect on microwaves that passed through 50 superclusters and 50 supervoids mapped at various places on the sky by the Sloan Digital Sky Survey. The microwaves come from the cosmic microwave background (CMB) radiation — the blotched-looking image at right that is our earliest picture of the universe, originating when matter and light separated a mere 380,000 years after the Big Bang.
Because temperature fluctuations existed in the CMB even before the radiation passed through later superstructures, the astronomers had to find a way to reveal the ISW effect hiding in this "noise." They did so by stacking CMB images of the sky that correspond to superstructures' locations.
"Each time you add another image to the stack, the CMB fluctuations average out, thus get smaller, and our desired ISW signal gets stronger," explains Szapudi. Summing up the stacks, the scientists found that slightly warm and cool spots on the microwave background indeed line up with superclusters and supervoids, respectively. The spots' sizes and strengths across cosmic ages match what accelerating expansion predicts.
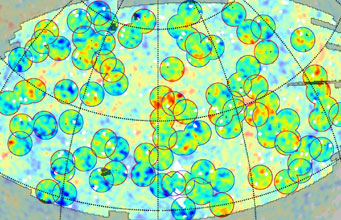
The positions of known supervoids and superclusters is overlaid on the WMAP data. The blue circles mark supervoids, the red ones superclusters.
U of Hawaii: B. Granett, M. Neyrinck, I. Szapudi
Scientists have studied the ISW effect before, and the Hawaii group's results bring us no closer to understanding dark energy's nature, says Mario Livio (Space Telescope Science Institute). Still, the study supports other teams' work, particularly theories that the prominent "Cold Spot" — a (you guessed it) very cold region on the CMB discovered in 2004 — results from a supervoid (still unconfirmed, but more likely now). And the further evidence for dark energy's existence may be a solid step toward constraining current cosmological models, notes Sean Carroll (Caltech).
The paper, lead-authored by Benjamin Granett in collaboration with Szapudi and Mark Neyrinck, will appear in a future issue of the Astrophysical Journal Letters.
More information is in an Institute for Astronomy press release, along with some great images and animations.
 27
27









Comments
Chris
August 8, 2008 at 10:59 am
"a conveniently ambiguous term for something no one understands"
It is so refreshing to hear someone in the science media say that out loud.
You must be logged in to post a comment.
George Olshevsky
August 8, 2008 at 1:53 pm
I think the recent advances in cosmology have laid to rest a fundamental assumption about the shape of the universe, namely, the assumption that spacetime, before the formation of matter, had a uniform overall curvature on large scales (which matter messes up by its presence). We know that the presence of matter curves spacetime and changes geodesics from simple Euclidean straight lines to curves of various kinds, such as the helices described by orbiting planets. But suppose that, before there was matter, the universe came “pre-curved,” with regions of positive and negative curvature spread throughout, something like the bubbles in a sheet of bubble-wrap, only four-dimensional. Overall, viewed from an external perspective, the universe seems homogeneous, but up close, spacetime becomes a lattice of “hills” and “valleys,” the hills being regions of negatively curved spacetime and the valleys being regions of positively curved spacetime. Much like the earth, seen from far away, looks like a perfect sphere but nevertheless has its familiar hills and valleys and seas and continents once you zoom in for a closer look.
continued in next comment--
You must be logged in to post a comment.
George Olshevsky
August 8, 2008 at 1:54 pm
A region of positively curved spacetime would tend to accumulate matter, since geodesics (the path matter takes in free fall) tend to converge when their space is positively curved. As matter accumulates, the ambient positive curvature increases/ Contrariwise, a region of negatively curved spacetime would tend to disperse matter, since geodesics in negatively curved spaces tend to diverge. As matter flees the negatively curved voids, the ambient curvature tends ot decrease further (become more negative). These properties are strongly reminiscent of what we now see as galactic voids and clusters. If, at the Big Bang, the universe was a seething mess of relatively enormous spacetime-curvature quantum fluctuations (the Heisenberg uncertainty principle applies to spacetime curvature, which is equivalent to potential energy), these would have been frozen in place and greatly flattened out by Cosmic Inflation, resulting in very gently curved, enormous bubbles of positively curved spacetime within a filigree of gently negatively curved spacetime—without the need for any kinds of dark matter particles or dark energy. “Dark matter”simply mimics the properties of positively curved spacetime, “dark energy” mimics the properties of negatively curved spacetime. By present reckoning, about 73% of the volume of the visible universe is negatively curved, 27% positively curved, corresponding to the calculated magnitudes of “dark matter” and “dark energy.” And the regions of negative curvature appear to be expanding.
continued in next comment
You must be logged in to post a comment.
George Olshevsky
August 8, 2008 at 1:55 pm
We know that time runs slower, relative to an external observer, in regions of positively curved spacetime, to the point where it runs infinitely slowly (stops) at the event horizon of a black hole. Contrariwise, time should run faster, relative to an external observer, in regions of negatively curved spacetime. There seem to be no regions of extremely high negative curvature in the visible universe, so the speedup effect should be barely detectable in intergalactic voids if it exists. Or, the apparent acceleration of the universal expansion attributed to “dark energy” might in some way simply be an artifact of this time speedup.
You must be logged in to post a comment.
Allan Holmgren
August 8, 2008 at 10:18 pm
What an intriguing theory. I think you may be on to something here. One way we could look for this time speedup would be to catalogue a number of type II supernova's for a given class of stars in these regions of accellerated expansion and see if the fade-down times are shorter. If the overall majority of them are, this would indicate that this time speedup is the case.
You must be logged in to post a comment.
George Olshevsky
August 10, 2008 at 2:25 pm
The supernova test seems sound, but there may be trouble finding enough matter in a void to make a supernova(!). Perhaps an obliging galaxy, aimed properly, might stray into such a region every so often.
You must be logged in to post a comment.
George Olshevsky
August 10, 2008 at 2:27 pm
Some further interesting properties of negatively-curved (hyperbolic) regions of spacetime include the opposite of “gravitational redshift,” namely, “antigravitational blueshift.” Photons emerging from a source inside a region of negative spacetime curvature should have their frequencies increased. This is equivalent to the “time speedup” effect described previously... continued in next comment...
You must be logged in to post a comment.
George Olshevsky
August 10, 2008 at 2:29 pm
Left to itself, without interference from matter, positively curved spacetime is unstable and will in time contract to a singularity. Contrariwise, negatively curved spacetime will in time expand forever, “trying” to become Euclidean by making its curvature “less negative.”. In our universe, the latter effect helps to keep the former effect from dominating and collapsing the universe into a black hole. This also perhaps accounts for why there are no apparent regions of highly curved hyperbolic spacetime: they rapidly expanded—and are probably doing so even now—and "flattened out." ...concluded in next comment...
You must be logged in to post a comment.
George Olshevsky
August 10, 2008 at 2:29 pm
Left to itself, without interference from matter, positively curved spacetime is unstable and will in time contract to a singularity. Contrariwise, negatively curved spacetime will in time expand forever, “trying” to become Euclidean by making its curvature “less negative.”. In our universe, the latter effect helps to keep the former effect from dominating and collapsing the universe into a black hole. This also perhaps accounts for why there are no apparent regions of highly curved hyperbolic spacetime: they rapidly expanded—and are probably doing so even now—and "flattened out." ...concluded in next comment...
You must be logged in to post a comment.
George Olshevsky
August 10, 2008 at 2:30 pm
If you construct a sphere in Euclidean (“flat”) space, its volume will always be pi times the radius squared. In positively curved space, the volume of a like sphere will always exceed pi times the radius squared, and in negatively curved space, the volume will always fall short of pi times the radius squared. I can see no theoretical reason that the volume inside the former cannot be made as large as we like, nor do I see any theoretical reason that the volume inside the latter cannot be made as small as zero, for any given radius greater than zero.
You must be logged in to post a comment.
George Olshevsky
August 10, 2008 at 3:29 pm
Left to itself, without interference from matter, positively curved spacetime is unstable and will in time contract to a singularity. Contrariwise, negatively curved spacetime will in time expand forever, “trying” to become Euclidean by making its curvature “less negative.”. In our universe, the latter effect helps to keep the former effect from dominating and collapsing the universe into a black hole. This also perhaps accounts for why there are no apparent regions of highly curved hyperbolic spacetime: they rapidly expanded—and are probably doing so even now—and flattened out. ...concluded in next comment
You must be logged in to post a comment.
George Olshevsky
August 10, 2008 at 3:31 pm
If you construct a sphere in Euclidean (“flat”) space, its volume will always be pi times the radius squared. In positively curved space, the volume of a like sphere will always exceed pi times the radius squared, and in negatively curved space, the volume will always fall short of pi times the radius squared. I can see no theoretical reason that the volume inside the former cannot be made as large as we like, nor do I see any theoretical reason that the volume inside the latter cannot be made as small as zero, for any given radius greater than zero.
You must be logged in to post a comment.
George Olshevsky
August 10, 2008 at 5:21 pm
If you construct a sphere in Euclidean (“flat”) space, its volume will always be pi times the radius squared. In positively curved space, the volume of a like sphere will always exceed pi times the radius squared, and in negatively curved space, the volume will always fall short of pi times the radius squared. Unless I’m much mistaken (which I’ve been lamentably often in the past), I can see no theoretical reason that the volume inside the former cannot be made as large as we like, nor do I see any theoretical reason that the volume inside the latter cannot be made as small as zero, for any given radius greater than zero. (Sorry for hogging the comments with all this stuff, and begging your indulgence.)
You must be logged in to post a comment.
George Olshevsky
August 10, 2008 at 5:21 pm
If you construct a sphere in Euclidean (“flat”) space, its volume will always be pi times the radius squared. In positively curved space, the volume of a like sphere will always exceed pi times the radius squared, and in negatively curved space, the volume will always fall short of pi times the radius squared. Unless I’m much mistaken (which I’ve been lamentably often in the past), I can see no theoretical reason that the volume inside the former cannot be made as large as we like, nor do I see any theoretical reason that the volume inside the latter cannot be made as small as zero, for any given radius greater than zero. (Sorry for hogging the comments with all this stuff, and begging your indulgence.)
You must be logged in to post a comment.
George Olshevsky
August 10, 2008 at 6:51 pm
If you construct a sphere in Euclidean (“flat”) space, its volume will always be pi times the radius squared. In positively curved space, the volume of a like sphere will always exceed pi times the radius squared, depending on the local curvature of the space and the radius of the sphere, and in negatively curved space, the volume will always fall short of pi times the radius squared. Unless I’m much mistaken (which I’ve been lamentably often in the past), I can see no theoretical reason that the volume inside the former cannot be made as large as we like, nor do I see any theoretical reason that the volume inside the latter cannot be made as small as zero, for any given radius greater than zero. (Sorry for hogging the comments here; I beg your indulgence.)
You must be logged in to post a comment.
George Olshevsky
August 10, 2008 at 6:51 pm
If you construct a sphere in Euclidean (“flat”) space, its volume will always be pi times the radius squared. In positively curved space, the volume of a like sphere will always exceed pi times the radius squared, depending on the local curvature of the space and the radius of the sphere, and in negatively curved space, the volume will always fall short of pi times the radius squared. Unless I’m much mistaken (which I’ve been lamentably often in the past), I can see no theoretical reason that the volume inside the former cannot be made as large as we like, nor do I see any theoretical reason that the volume inside the latter cannot be made as small as zero, for any given radius greater than zero. (Sorry for hogging the comments here; I beg your indulgence.)
You must be logged in to post a comment.
George Olshevsky
August 11, 2008 at 10:09 am
If you construct a sphere in Euclidean (“flat”) space, its volume will always be 4/3 pi times the radius cubed. In positively curved space, the volume of a like sphere will always exceed 4/3 pi times the radius cubed, depending on the local curvature of the space and the radius of the sphere, whereas in negatively curved space, the volume will always fall short of 4/3 pi times the radius cubed. Unless I’m much mistaken (which I’ve been lamentably often in the past), I can see no theoretical reason that the volume inside the former cannot be made as large as we like, nor do I see any theoretical reason that the volume inside the latter cannot be made as small as zero, for any given radius greater than zero. The difference between the actual volume inside the sphere and the volume of a Euclidean sphere of the same radius provides a kind of measure for how curved the local space is. (Sorry for hogging all this comment space; I beg your indulgence.)
You must be logged in to post a comment.
George Olshevsky
August 12, 2008 at 11:54 am
Please ignore previous post, which went out before I had a chance to vet it. Here is a corrected version: If you construct a sphere in Euclidean (“flat”) space, its volume will always be 4/3 pi times the radius cubed. In positively curved space, the volume of a like sphere will always exceed 4/3 pi times the radius cubed, depending on the local curvature of the space and the radius of the sphere, whereas in negatively curved space, the volume will always fall short of 4/3 pi times the radius cubed. Unless I’m much mistaken (which I’ve been lamentably often in the past), I can see no theoretical reason that the volume inside the former cannot be made as large as we like, nor do I see any theoretical reason that the volume inside the latter cannot be made as small as zero, for any given radius greater than zero. The difference between the volume inside the real sphere and a Euclidean sphere of the same radius provides a kind of measure of the local curvature of space. (Sorry for hogging the comments here; I beg your indulgence.)
You must be logged in to post a comment.
George Olshevsky
August 12, 2008 at 11:54 am
Please ignore previous post, which went out before I had a chance to vet it. Here is a corrected version: If you construct a sphere in Euclidean (“flat”) space, its volume will always be 4/3 pi times the radius cubed. In positively curved space, the volume of a like sphere will always exceed 4/3 pi times the radius cubed, depending on the local curvature of the space and the radius of the sphere, whereas in negatively curved space, the volume will always fall short of 4/3 pi times the radius cubed. Unless I’m much mistaken (which I’ve been lamentably often in the past), I can see no theoretical reason that the volume inside the former cannot be made as large as we like, nor do I see any theoretical reason that the volume inside the latter cannot be made as small as zero, for any given radius greater than zero. The difference between the volume inside the real sphere and a Euclidean sphere of the same radius provides a kind of measure of the local curvature of space. (Sorry for hogging the comments here; I beg your indulgence.)
You must be logged in to post a comment.
George Olshevsky
August 14, 2008 at 10:38 am
Please ignore the preceding; I posted it before completely vetting it. Here's the corrected version: If you construct a sphere in Euclidean (“flat”) space, its volume will always be 4/3 pi times the radius cubed, the radius being measured from an external viewpoint. In positively curved space, the volume of a like sphere from a like viewpoint will always exceed 4/3 pi times the radius cubed, by an amount depending on the local curvature of the space and the radius of the sphere, whereas in negatively curved space, the volume will always fall short of 4/3 pi times the radius cubed. Unless I’m much mistaken (which I’ve been lamentably often in the past), I can see no theoretical reason that the volume inside the former cannot be made as large as we like, nor do I see any theoretical reason that the volume inside the latter cannot be made as close to zero as we like, for any given radius greater than zero. The difference between the volume inside the real sphere and a Euclidean sphere of the same radius provides a kind of measure of the local curvature of space. It is only when the sphere straddles a boundary between regions of positively and negatively curved space that its volume may become 4/3 pi times the radius cubed, just as if the space in which it is imbedded were Euclidean. This makes me imagine that on the average, the Universe could be a Euclidean space, even though its more finely detailed structure would consist of bubble-wrap regions of positively and negatively curved space. (Sorry for hogging the comments here; I beg your indulgence.)
You must be logged in to post a comment.
George Olshevsky
August 14, 2008 at 10:38 am
Please ignore the preceding; I posted it before completely vetting it. Here's the corrected version: If you construct a sphere in Euclidean (“flat”) space, its volume will always be 4/3 pi times the radius cubed, the radius being measured from an external viewpoint. In positively curved space, the volume of a like sphere from a like viewpoint will always exceed 4/3 pi times the radius cubed, by an amount depending on the local curvature of the space and the radius of the sphere, whereas in negatively curved space, the volume will always fall short of 4/3 pi times the radius cubed. Unless I’m much mistaken (which I’ve been lamentably often in the past), I can see no theoretical reason that the volume inside the former cannot be made as large as we like, nor do I see any theoretical reason that the volume inside the latter cannot be made as close to zero as we like, for any given radius greater than zero. The difference between the volume inside the real sphere and a Euclidean sphere of the same radius provides a kind of measure of the local curvature of space. It is only when the sphere straddles a boundary between regions of positively and negatively curved space that its volume may become 4/3 pi times the radius cubed, just as if the space in which it is imbedded were Euclidean. This makes me imagine that on the average, the Universe could be a Euclidean space, even though its more finely detailed structure would consist of bubble-wrap regions of positively and negatively curved space. (Sorry for hogging the comments here; I beg your indulgence.)
You must be logged in to post a comment.
Stephen Crothers
September 1, 2008 at 7:54 pm
Einstein’s field equations for the static vacuum gravitational field, i.e. Ric = 0,violate his ‘Principle of Equivalence’ – the equivalence of gravitational and inertial mass, and the laws of SR, cannot manifest in a spacetime which is by definition empty. So if his energy-momentum tensor is zero there is no gravitational field and his field equations become:
Gij/k + Tij = 0, (subscripts)i,j = 0,1,2,3, k = constant,
where Gij/k are the components of a gravitational energy tensor. The total energy of the gravitational field is always zero; Gij/k and Tij vanish identically; there is no possibility for the localisation of gravitational energy (i.e. no gravitational waves). Also, Einstein’s GR violates the experimentally well established conservation of energy and momentum, so if the usual conservation of energy and momentum is valid (there is no experimental evidence to refute it) then GR is invalid. Einstein invented his pseudo-tensor by which he and subsequent big bangers claim that his gravitational energy can be localized. However, his pseudo-tensor is a meaningless concoction of mathematical symbols because it implies the existence of a 1st-order intrinsic differential invariant which depends only upon the components of the metric tensor and their 1st-derivatives (contract his pseudo-tensor and apply Euler’s theorem). But the pure mathematicians Ricci-Curbastro and Levi-Civita proved in 1900 that such invariants do not exist! Einstein and subsequent big bangers resort to linearisation of Einstein’s field equations to localize his gravitational energy. This is nonsense because linearisation implies the existence of a tensor which, except for being precisely zero, does not otherwise exist, as proven by H. Weyl in 1944. So LIGO, AIGO and VIRGO are destined to detect nothing.
http://www.sjcrother.plasmaresources.com/Unicorns.pdf
http://www.ptep-online.com/index_files/2007/PP-09-14.PDF
http://www.ptep-online.com/index_files/2008/PP-12-11.PDF
You must be logged in to post a comment.
Wayne
November 30, 2009 at 1:04 pm
Here is an alternative to dark energy. For the sake of discussion, letâs make two assumptions. First, the universe is expanding. Second, gravity is slowing down the rate of expansion.
Now letâs imagine what we would observe if these two assumptions were true. Distant galaxies would appear to be expanding away from us at a rate of expansion from the distant past. Galaxies near to us would be expanding away from us at a rate of expansion from the near past. When we observe an object at a distance of 13.5 billion light years; we are observing what happened 13.5 billion years ago in the past.
Observing distant galaxies expanding away from us at a faster rate that nearby galaxies is exactly what we are observing. We should be interpreting this as evidence that the rate of expansion is slowing down, and there is no dark energy.
Finding the rate of slowdown of the expanding universe will require relativistic calculations, since most of the observable galaxies are traveling at a significant fraction of the speed of light.
You must be logged in to post a comment.
Wayne
November 30, 2009 at 1:04 pm
Here is an alternative to dark energy. For the sake of discussion, letâs make two assumptions. First, the universe is expanding. Second, gravity is slowing down the rate of expansion.
Now letâs imagine what we would observe if these two assumptions were true. Distant galaxies would appear to be expanding away from us at a rate of expansion from the distant past. Galaxies near to us would be expanding away from us at a rate of expansion from the near past. When we observe an object at a distance of 13.5 billion light years; we are observing what happened 13.5 billion years ago in the past.
Observing distant galaxies expanding away from us at a faster rate that nearby galaxies is exactly what we are observing. We should be interpreting this as evidence that the rate of expansion is slowing down, and there is no dark energy.
Finding the rate of slowdown of the expanding universe will require relativistic calculations, since most of the observable galaxies are traveling at a significant fraction of the speed of light.
You must be logged in to post a comment.
Wayne
November 30, 2009 at 1:06 pm
The discrepancies in mass measurements can be totally explained by black holes. Black holes could be much more numerous than we believe, since they are difficult to observe. Many novas end up as black holes, and black holes are extremely acquisitive when it comes to acquiring any and all matter in their local vicinity.
X-ray telescopes give us an excellent indication of the mass of the protons and neutrons are in a galaxy or galaxy cluster. X-rays cannot, however, tell us anything about the mass in black holes. One of the main proofs for dark matter is that X-ray photographs indicate less mass in a galaxy cluster than does gravitational lensing. The missing mass could readily be explained by black holes.
Another proof of dark matter is that the galaxies and clusters should be rotating slower based upon the mass indicated by the X-ray telescopes. Again, this discrepancy could be explained by a higher prevalence of black holes than expected.
You must be logged in to post a comment.
Wayne
November 30, 2009 at 1:06 pm
The discrepancies in mass measurements can be totally explained by black holes. Black holes could be much more numerous than we believe, since they are difficult to observe. Many novas end up as black holes, and black holes are extremely acquisitive when it comes to acquiring any and all matter in their local vicinity.
X-ray telescopes give us an excellent indication of the mass of the protons and neutrons are in a galaxy or galaxy cluster. X-rays cannot, however, tell us anything about the mass in black holes. One of the main proofs for dark matter is that X-ray photographs indicate less mass in a galaxy cluster than does gravitational lensing. The missing mass could readily be explained by black holes.
Another proof of dark matter is that the galaxies and clusters should be rotating slower based upon the mass indicated by the X-ray telescopes. Again, this discrepancy could be explained by a higher prevalence of black holes than expected.
You must be logged in to post a comment.
Wayne
November 30, 2009 at 1:08 pm
Iâve also recently read that the age of the Universe is estimated to be in the vicinity of 13.5 to 14 billion years old, with the best guess being 13.7 billion years old. The most distant observable object is 13.5 billion light years away. I have not read this, but it seems that astronomers are equating the edge of observability with the edge of the Universe. The proposed JWST, the James Webb Space Telescope, is supposed to be able to see all the way to beginning of time (the edge of the Universe).
I think that OS (my own acronym for observable space) is a sphere with a radius of 13.7 light years and our solar system at the center. Objects more distant than 13.7 light years will be receding away from us faster than the speed of light and, thus, their light emissions could never reach us.
If OS were really the entire Universe, then the big bang would have originated near our solar system. Centuries ago astronomers have abandoned the belief that Earth is the center of the Universe. The Universe may have existed much longer than 13.7 billion years. Our observations may be restricted to a tiny bubble in the midst of an unimaginably vast Universe.
Shortly after Schwarzschild informed Einstein about the theoretical discovery of black holes with the gravity waves bending back in on themselves, Einstein conjectured that the infinitely massive universe might be finite with its gravity waves bending back in on itself. Just like a black hole. This was never backed up with calculations and cannot be taken as proof that the universe is only 13.7 billion years old.
You must be logged in to post a comment.
You must be logged in to post a comment.