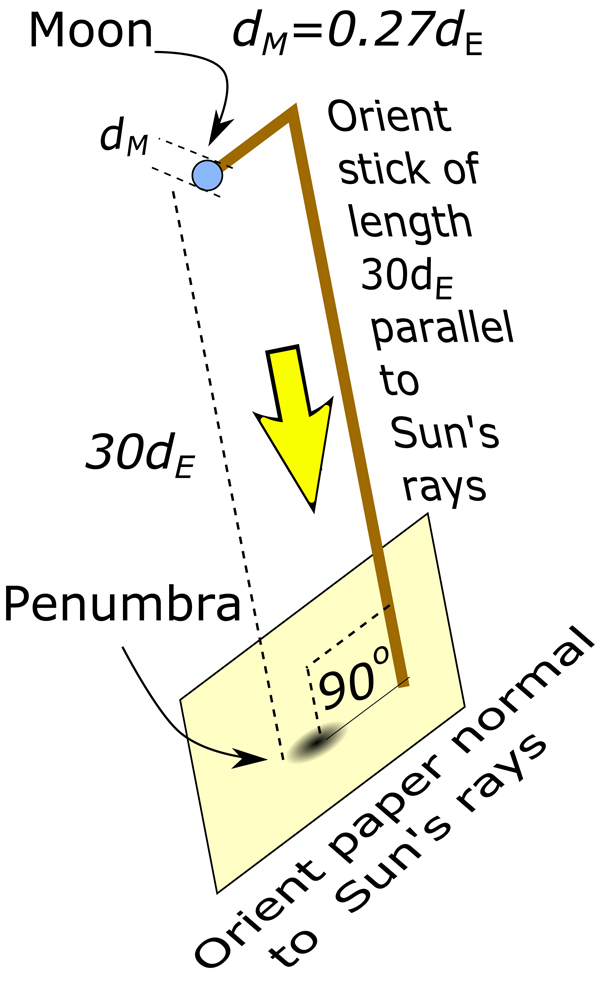
Here’s a fun experiment you can do with older kids 0r students on a sunny day this summer. All you’ll need is a small sphere attached to a stick held high above your head and something white on the ground, like a sheet of paper, where you can project the shadow. We used a one-inch-wide Styrofoam ball and held it 110 inches above the ground. This creates a scale model, with the small sphere representing the Moon, and the sheet of paper representing Earth’s surface.
This experiment will help participants understand how ancient Greek scientists measured the size and distance to the Moon. It follows the method of Hipparchus, who showed that the size of the Moon plays a key role in determining the size of the penumbra on Earth during a solar eclipse. The penumbra is the part of the Moon’s shadow where some of the Sun is still visible. It’s Latin for “almost shade”: think peninsula (“almost island”) and umbrella (which provides shade).

Guy Vandegrift
Make the distance from the small sphere to the sheet of paper about 110 times larger than the diameter of the sphere. To represent Earth, draw a circle on the paper with a diameter that is 3.67 times larger than that of the small sphere. You will use the actual light from the Sun to make your mini-eclipse.
Key to this experiment, and what makes a solar eclipse so spectacular, is that the Sun and Moon have nearly identical angular sizes. Were the Moon farther away from Earth, it would not fully cover up the Sun. Were it closer, we would not see the Sun’s corona as the Moon passed between Earth and the Sun. This relationship between these nearly equal angular sizes ensures that the umbra (totality) of the solar eclipse will be very small, or even nonexistent in the case of an annular eclipse.
For best results, point the stick at the Sun so that it makes little or no shadow, but don’t worry too much about precision. With a one-inch-diameter Moon, the actual scaled distance might differ by as much as plus or minus 6 inches from the nominal value of 110 inches (primarily due to the elliptical nature of the Moon’s orbit). Also, if the Sun is not high in the sky, near zenith, the paper should be oriented to face the Sun’s rays. This orientation is not very critical; if the shadow does not look elliptical, the paper is sufficiently well oriented. You need to attach the sphere to the stick in a way that the sphere protrudes outward from the stick a bit. We used a pair of lab clamps about the thickness of a pencil (which caused the two shadows seen in the photo). Also, there’s no reason you can’t replace the sphere by a small disk, provided it is oriented properly.
Guy Vandegrift
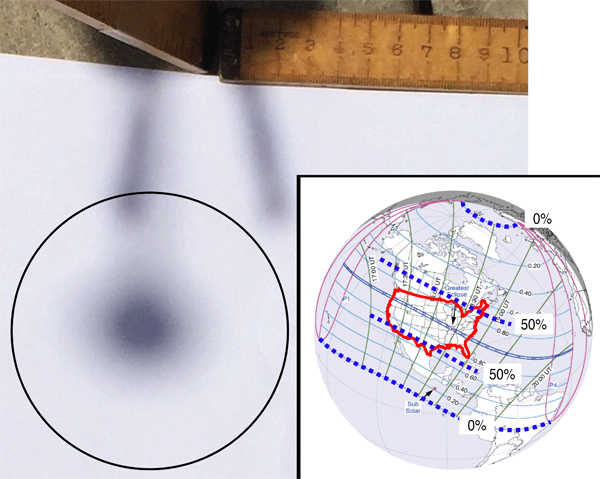
We used an Apple iPhone 6 Plus to photograph the shadow, and imported the digital image into Inkscape where we could add a circle 3.67 inches in diameter (9.3 cm) using the ruler shown in the photo. The penumbra looks like a “fuzzy shadow”, with an edge that is difficult, if not impossible to discern.
We also imported an image provided by NASA showing the penumbra for the upcoming solar eclipse (August 21, 2017) into our Inkscape file, and resized it to match the scale of our photo. The dotted blue lines indicate portions on the penumbra where 50% of the Sun is blocked, and the edge of the penumbra where essentially 0% is blocked, and no eclipse would be visible. You can see that the fuzzy shadow is slightly smaller than indicated by the range of the predicted penumbra. This is most likely due to fact that the shadow is not visible near locations where essentially 0% of the Sun is blocked.
This lab resembles the work of Hipparchus (190-125 B.C.) who used information about the penumbra during a solar eclipse to estimate the size of the Moon. Of course, no NASA map was available to measure the penumbra’s size. Instead, Hipparchus cleverly applied Euclidean geometry to the fact that 80% of the Sun was blocked in Alexandria during an eclipse that was observed to be total in another city (believed by many to be in the Hellespont, along the northwest coast of Turkey).
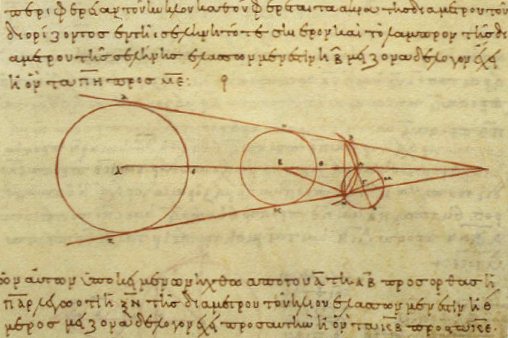
Anybody interested in a challenge might try to capture the size of the umbra during a simulated lunar eclipse by letting a larger sphere represent Earth, with the paper on the ground representing the space through which the Moon moves during a lunar eclipse. This would follow the earlier work of Aristarchus of Samos (310-230 B.C.). As shown in this 10th-century copy of one of his drawings, Aristarchus used the passage of the Moon through the Earth’s umbra during a lunar eclipse to glean information where the Moon was when it passed through Earth’s shadow. This is likely to be a much more difficult experiment: The umbra should be a portion of the shadow that has uniform greyness.
I teach astronomy, and did this experiment because I want others to attempt it. Send in your comments and photos, even ones with complications and unexpected results. It’s the surprises that make experimental science fun!
References
- Carman, Christián C. "Two problems in Aristarchus’s treatise on the sizes and distances of the sun and moon."Archive for history of exact sciences 1 (2014): 35-65.
- Hon, Giora. "Is there a concept of experimental error in Greek astronomy?" The British Journal for the History of Science 22.02 (1989): 129150.
- Toomer, Gerald J. "Hipparchus on the distances of the sun and moon."Archive for History of Exact Sciences 2 (1974): 126-142.
 0
0










Comments
You must be logged in to post a comment.