This year’s award goes to three researchers who played key roles in developing the theoretical and observational evidence for black holes.
For the second time in four years, black holes have nabbed the Nobel Prize in Physics. The 2020 prize, announced earlier today, recognizes the contributions of three researchers who have helped clinch the case for black holes’ existence: physicist Roger Penrose (University of Oxford, UK) and astronomers Reinhard Genzel (Max Planck Institute for Extraterrestrial Physics, Germany) and Andrea Ghez (University of California, Los Angeles).
Penrose will receive half of the 10 million Swedish kronor ($1.1 million U.S.) prize; Genzel and Ghez will share the other half equally.
Together, these three scientists have helped revolutionize our knowledge of black holes.

The Singularity: Resistance Is Futile
We know today that black holes are an unavoidable consequence of Albert Einstein’s general theory of relativity. In this framework, gravity is geometry: Mass tells spacetime how to curve, and spacetime’s curves tell mass how to move. Black holes are where mass curves spacetime so much that nothing, not even light, can escape.
Technically, the concept of a dense object from which light can’t escape predates Einstein. The English priest and scientist John Michell and the French polymath Pierre-Simon Laplace independently suggested the idea in the late 1700s. But it was the German astronomer Karl Schwarzschild who laid the groundwork for black holes as we know them today, when he solved Einstein’s equations for how a symmetric, nonrotating, and hefty mass would curve the spacetime around it — all while on a World War I battlefront in early 1916.
Black holes would not be scientifically palatable, however, for several decades.
In 1939, calculations by American physicist Robert Oppenheimer and his student Hartland Snyder showed that an astronomical body will inevitably contract to a singularity of infinite density in certain cases of spherically symmetric collapse. An event horizon would surround the singularity, closing the interior off from the outside universe. (Einstein loathed the idea.) New Zealand mathematician Roy Kerr expanded the work to rotating objects in 1963.
But it was Penrose in the mid-1960s who generalized the idea: He showed that collapse to a singularity always happens when there’s enough mass/energy packed together, regardless of the symmetry of the collapse.
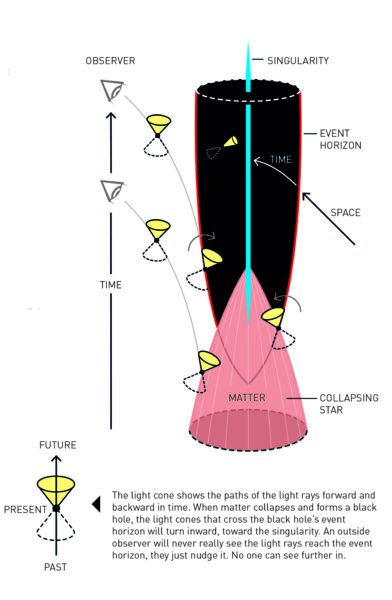
© Johan Jarnestad / The Royal Swedish Academy of Sciences
Penrose introduced a new mathematical concept to make this leap: trapped surfaces. A trapped surface forces all rays perpendicular to it to converge, regardless of whether the surface curves inwards or outwards. Light cannot escape; it can only stand still. And since nothing can travel faster than light, everything else falls in. The path inward is as inexorable as the forward arrow of time outside the black hole: one-way traffic only.
The unavoidable outcome is a singularity — which, for related reasons, is sometimes described as a single moment in time. It remains unclear what the singularity actually is. All we know is, it’s there that classical physics breaks down. (In gravity terms, spacetime becomes infinitely curved.)
Among his other contributions, Penrose also discovered that it’s possible to extract energy from a spinning black hole. Place a heavy mug on a cloth napkin and twist the mug. The napkin will twist with the mug, creating a warped cloth landscape. Something similar happens with a spinning black hole: It drags the fabric of spacetime around with it, in what’s called the Lense-Thirring effect. (Earth does this, too, but not as severely.)
The twisted region is called the ergosphere. Here, an astronaut (or asteroid, or any other object) would be forcibly dragged around with the black hole’s rotation, even though they were outside the event horizon. Penrose realized that it’s possible to steal rotational energy from the black hole via the ergosphere. Others have since used this insight to suggest that spin energy is how black holes power their relativistic jets, some of which shoot across thousands of light-years.

ESO / L. Calçada
To Boldly Go Where No One Has Gone Before
Penrose’s work helped explain how black holes could power distant, stupendously luminous sources discovered during the same years he was working on the singularity problem in the 1960s. These quasars were the first observational evidence of black holes. But it would take several decades for astronomers to amass the observations to convince themselves that supermassive black holes sit at the center of nearly every major galaxy. The objects even have a strangely symbiotic relationship with their hosts.
Genzel and Ghez’s work was pivotal in this effort. Thanks to a series of technical feats they either developed or took advantage of, the two astronomers and their competing teams have spent nearly three decades using the world’s best ground-based infrared telescopes to peer through the dusty gas of our galaxy’s center. Here, deep in the heart of the Milky Way, they saw dozens of stars looping pell-mell around an invisible center. By tracing the stars’ motions over years, the astronomers mapped out the stars’ orbits — which, it must be emphasized, is no mean feat: These stars are more than 26,000 light-years away and crowd together in the field of view like moving polka dots.
The orbits revealed that the stars revolve around an unseen, unmoving, and compact something-or-other with the mass of 4 million Suns. The best explanation is a supermassive black hole, which astronomers call Sagittarius A*.
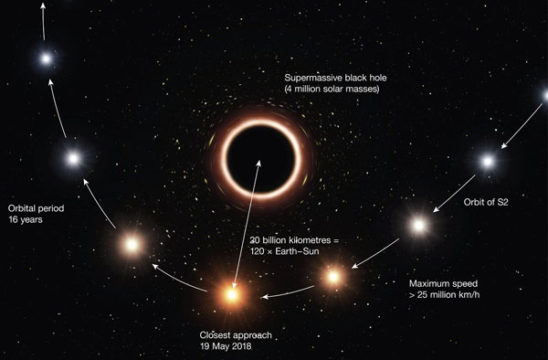
ESO / M. Kornmesser
The teams’ observations have also enabled them to confirm two predictions of general relativity: gravitational redshift and orbital precession. As the star S2 (S0-2 in the Ghez team’s nomenclature) bore down on Sgr A* in 2018, it dipped into the spacetime valley the black hole makes around itself. During this time, the star’s light had to work harder to climb out and reach us. The energy loss reddened the light, which both teams detected.
Traveling through the warped spacetime also shifted the star’s path slightly. Its incoming angle changed by a tiny amount, which in turn changed the location of its closest approach to the black hole. Over many passes, the star’s orbit will trace out a rosette shape instead of a single ellipse. Genzel’s team reported the first evidence of this shift earlier this year.
Astronomers both inside and outside the teams credit the longstanding competition between the two groups for driving them to excellence. Their results — arrived at with independent methods and observations — also provide a beautiful confirmation of each other’s analyses that can be hard to come by in science.
In short, the three newly minted Nobel laureates are remarkable scientists. But the real winners, one might argue, are black holes. A century ago, they were math on paper; now, they’re as common in the cosmos as dust bunnies under a couch. Genzel, Ghez, and Penrose helped make that happen.
The Nobel Committee for Physics has released two excellent write-ups of the winners’ work: a detailed explanation for the public and a more technical scientific background document. These both go into far more detail than I have here, and I encourage you to read them — not just about these awards, but on any topic that’s received a Nobel: The prize committee write-ups are often superb sources of information.
 1
1









Comments
Gg
October 11, 2020 at 7:56 am
Thanks for the well written article. I always thought that Penrose was a mathematician.
You must be logged in to post a comment.
You must be logged in to post a comment.